The resistance 4R,16R,64R....∞ are connected in series. Find their equivalent resistance.
To find the equivalent resistance of the resistors connected in series (4R, 16R, 64R, ...), we can follow these steps:
Step 1: Identify the series resistance formula
In a series circuit, the total or equivalent resistance (R_eq) is the sum of all individual resistances. The formula is:
Req=R1+R2+R3+...
Step 2: Write down the resistances
The resistances given are in the form of a geometric series:
- First resistance, R1=4R
- Second resistance, R2=16R
- Third resistance, R3=64R
- And so on...
Step 3: Identify the pattern of the series
The resistances can be expressed as:
- R1=4R=4R
- R2=16R=4R⋅4
- R3=64R=4R⋅16
This shows that each resistance can be written as 4R⋅4n for n=0,1,2,...
Step 4: Sum the series
The resistances can be expressed as:
Req=4R+16R+64R+...
This is a geometric series where:
- First term a=4R
- Common ratio r=4
The sum of an infinite geometric series can be calculated using the formula:
S=a1−r
where |r|<1.
However, in this case, since r=4 (which is greater than 1), the series diverges. This means that the equivalent resistance approaches infinity as more resistors are added.
Step 5: Conclusion
Thus, the equivalent resistance of the series of resistors 4R,16R,64R,... is:
Req=∞
In a series circuit, the total or equivalent resistance (R_eq) is the sum of all individual resistances. The formula is:
Req=R1+R2+R3+...
The resistances given are in the form of a geometric series:
- First resistance, R1=4R
- Second resistance, R2=16R
- Third resistance, R3=64R
- And so on...
The resistances can be expressed as:
- R1=4R=4R
- R2=16R=4R⋅4
- R3=64R=4R⋅16
The resistances can be expressed as:
Req=4R+16R+64R+...
This is a geometric series where:
- First term a=4R
- Common ratio r=4
S=a1−r
where |r|<1.
Thus, the equivalent resistance of the series of resistors 4R,16R,64R,... is:
Req=∞
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III26videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A32videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionFive equal resistance each of value R are connected in a circuit . Find equivalent resistance of the network between points A and C
 View Solution
View SolutionA voltmeter of resistance R1 and an ammeter of resistance R2 are connected in series across a battery oif negligible internal resistance. When as resistance R is connected in parallel to voltmeter reading of ammeter increases three times white that of voltmeter reduces to one third. Find the ratio of R1 and R2.
View SolutionSix equal resistance,eacch of resistance R are connected as shown in the figure.Equivalent resistance between P and Q is
_PHY_E05_276_Q01.png) View Solution
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R1+R2 and for (b) 1R'=1R1+1R2 and ΔR'R'2=ΔR1R21+ΔR2R22
View SolutionSix resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is
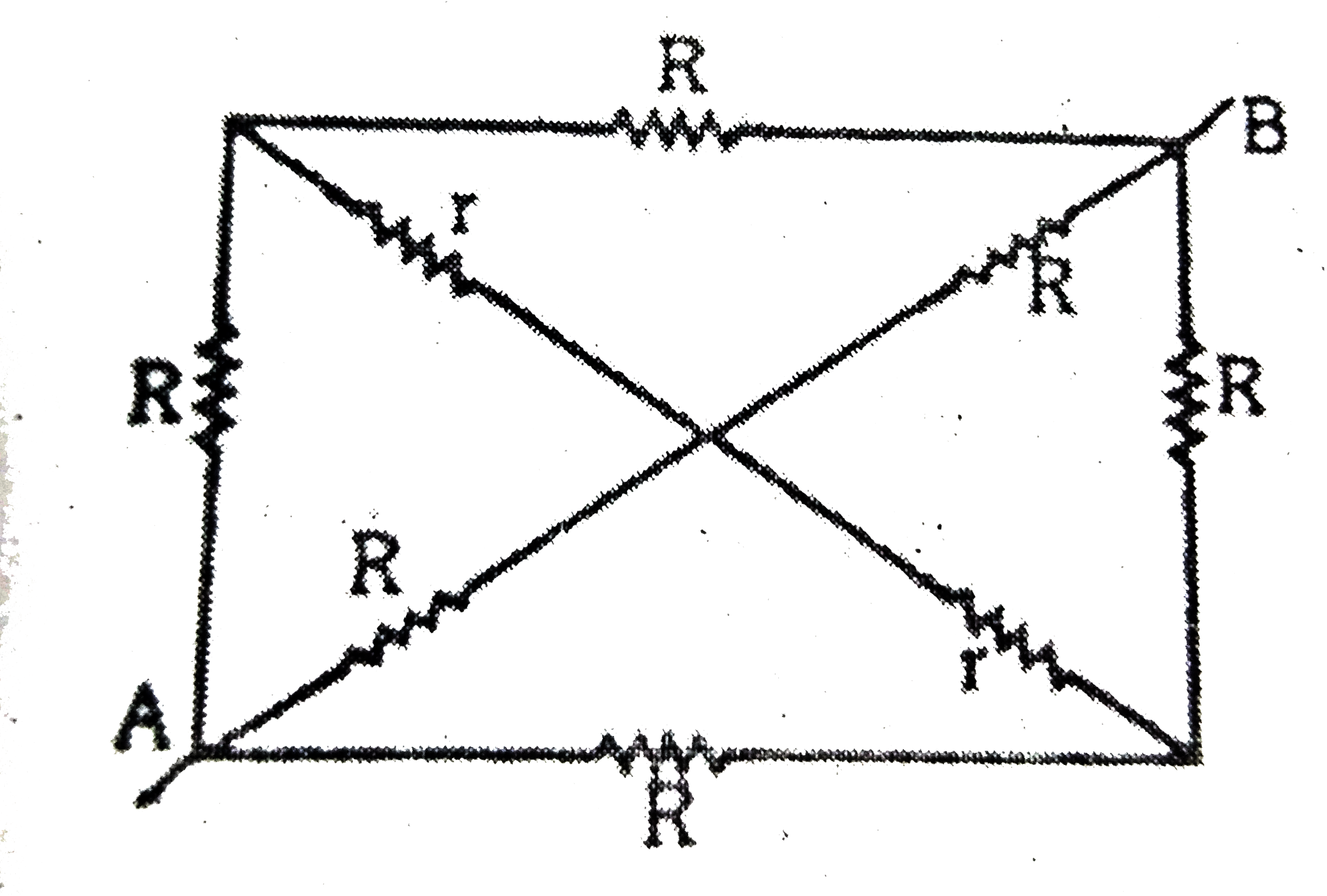 View Solution
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View Solution

