In a Wheatstone's brigde all the four arms have equal resistance R. If the resistance of the galvanometer arm is also R, the equivalent resistance of the combination as seen b the battery is
R
2R
R4
R2
The correct Answer is:A
To find the equivalent resistance of a Wheatstone bridge with all four arms having equal resistance R and the galvanometer arm also having resistance R, we can follow these steps:
Step 1: Understand the Wheatstone Bridge Configuration
In a Wheatstone bridge, there are four resistors arranged in a diamond shape. Let's label them as follows:
- Resistor P=R
- Resistor Q=R
- Resistor R=R
- Resistor S=R
The galvanometer is connected between the midpoints of the two pairs of resistors.
Step 2: Analyze the Balanced Condition
For a balanced Wheatstone bridge, the ratio of the resistances in one branch is equal to the ratio in the other branch:
PQ=RS
Since all resistors are equal, this condition is satisfied.
Step 3: Remove the Galvanometer Branch
In a balanced Wheatstone bridge, there is no current flowing through the galvanometer. Therefore, we can ignore the galvanometer branch for the purpose of calculating the equivalent resistance.
Step 4: Combine the Resistors in Series
The two pairs of resistors (P and Q, R and S) can be considered as two series combinations:
- The first series combination (P and Q) gives:
R1=R+R=2R
- The second series combination (R and S) gives:
R2=R+R=2R
Step 5: Combine the Series Combinations in Parallel
Now, we have two resistances R1 and R2 in parallel:
Req=11R1+1R2=112R+12R=122R=R2
Step 6: Conclusion
Thus, the equivalent resistance of the combination as seen by the battery is:
Req=R
Final Answer
The equivalent resistance of the combination as seen by the battery is R.
---
In a Wheatstone bridge, there are four resistors arranged in a diamond shape. Let's label them as follows:
- Resistor P=R
- Resistor Q=R
- Resistor R=R
- Resistor S=R
For a balanced Wheatstone bridge, the ratio of the resistances in one branch is equal to the ratio in the other branch:
PQ=RS
Since all resistors are equal, this condition is satisfied.
In a balanced Wheatstone bridge, there is no current flowing through the galvanometer. Therefore, we can ignore the galvanometer branch for the purpose of calculating the equivalent resistance.
The two pairs of resistors (P and Q, R and S) can be considered as two series combinations:
- The first series combination (P and Q) gives:
R1=R+R=2R
- The second series combination (R and S) gives:
R2=R+R=2R
Now, we have two resistances R1 and R2 in parallel:
Req=11R1+1R2=112R+12R=122R=R2
Thus, the equivalent resistance of the combination as seen by the battery is:
Req=R
The equivalent resistance of the combination as seen by the battery is R.
Similar Questions
In a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
View SolutionA uniform wire of resistance r is cut into n parts and they are connected in parallel. Effective resistance of the combination is
View Solution
Knowledge Check
Five equal resistances each of value R are connected in a form shown alongside. The equivalent resistance of the network
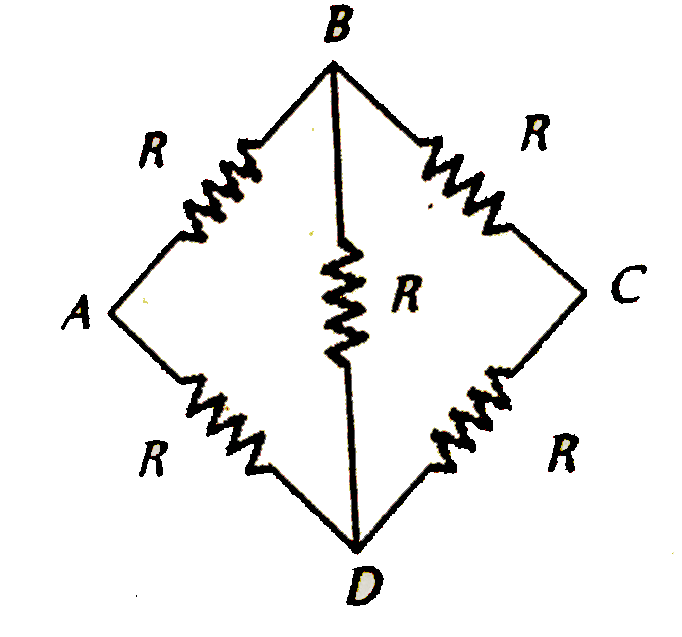 A12RB2RC58RD85R
A12RB2RC58RD85R
If each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
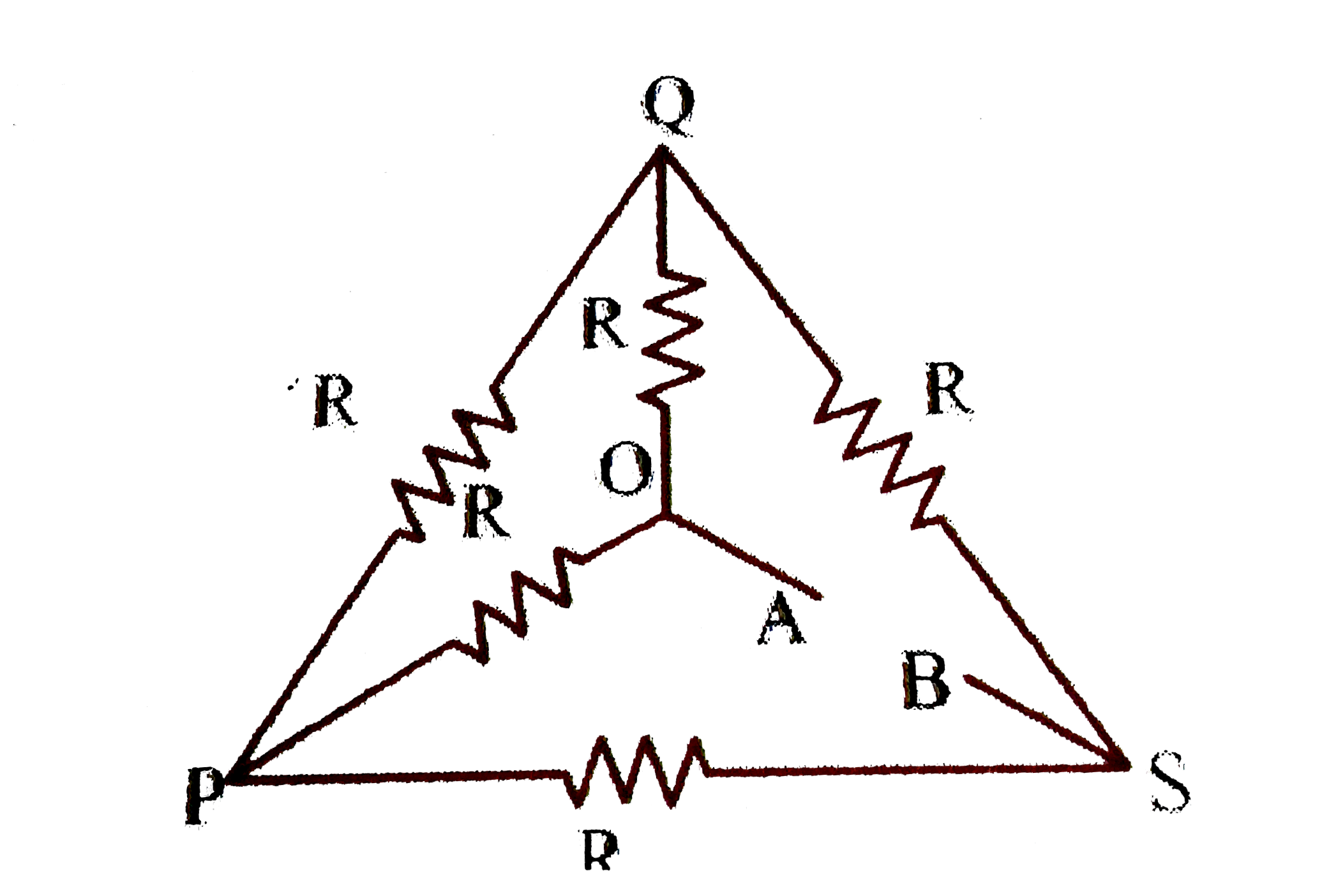
View SolutionIf each of the resistance in the network in figure R,
the equivalent resistance between terminals A and B is
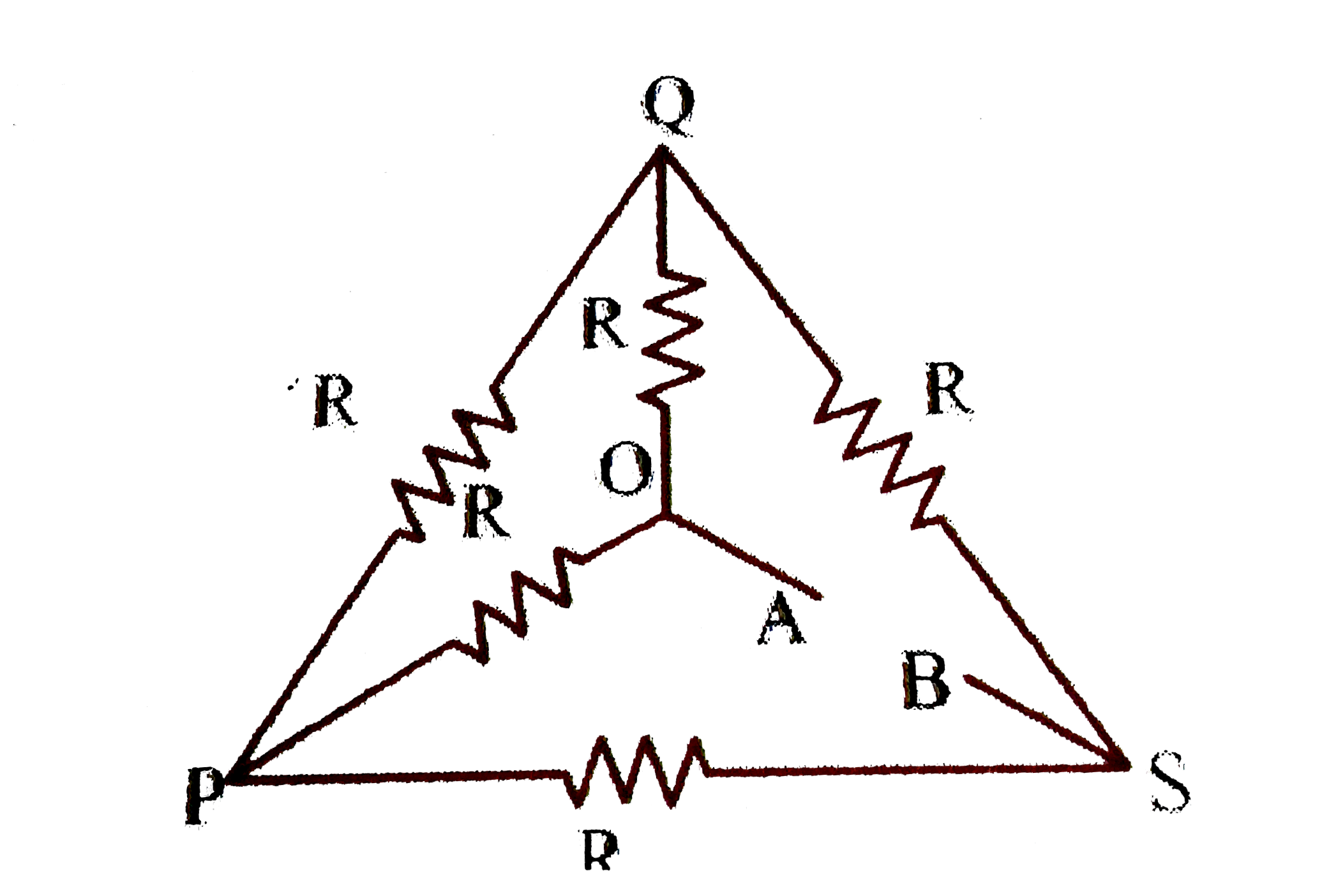
View SolutionSix equal resistance,eacch of resistance R are connected as shown in the figure.Equivalent resistance between P and Q is
_PHY_E05_276_Q01.png)
View SolutionResistance of each resistor is R. Then the equivalent resistance across A and B is

View Solution
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View SolutionA wire of resistance R is cut into ‘ n ’ equal parts. These parts are then connected in parallel. The equivalent resistance of the combination will be
View SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
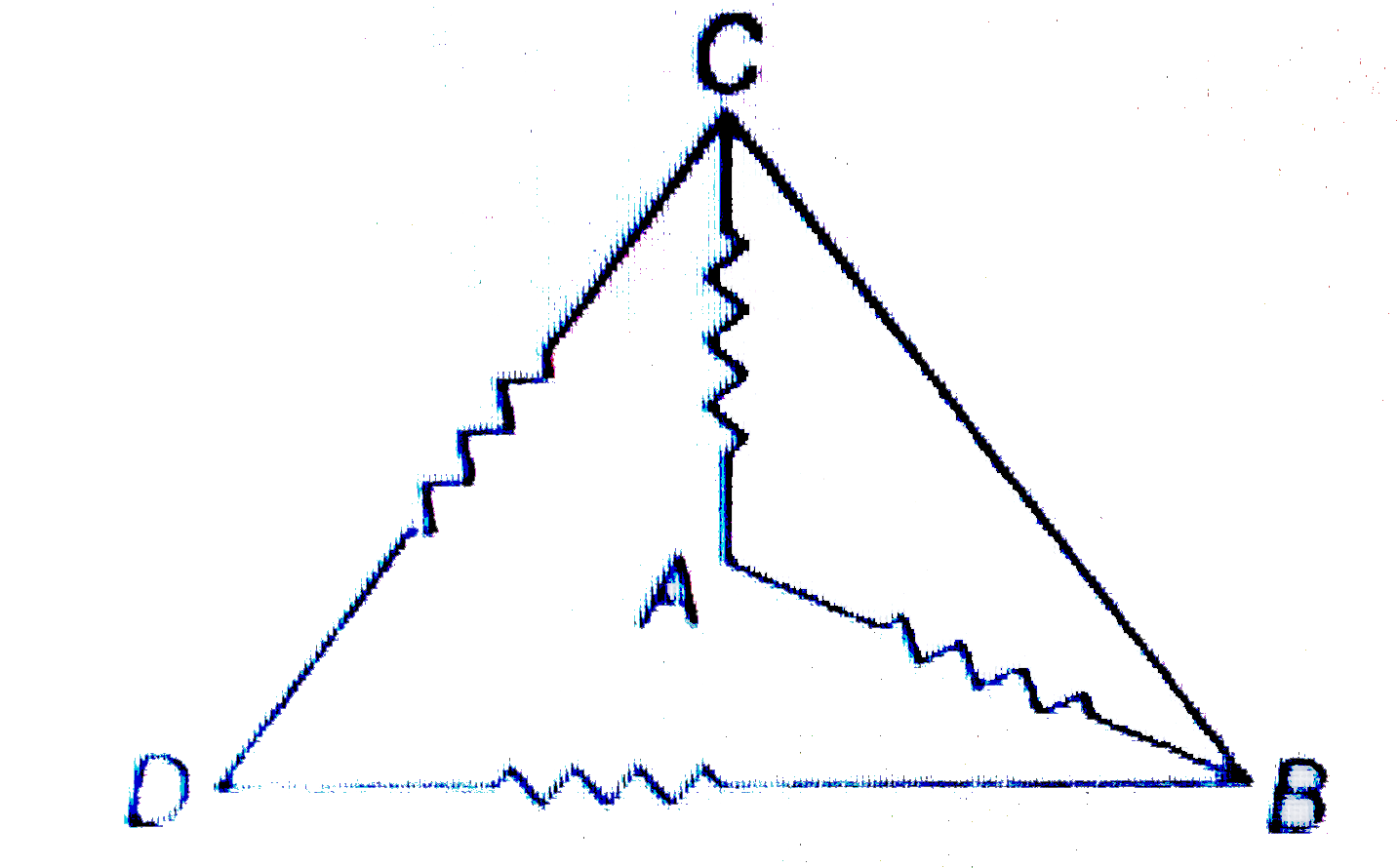
View Solution
