The magnetic field of a given length of wire carrying a current of a single turn circular coil at centre is B, then its value for two turns for the same wire when same current passing through it is
B4
B2
2B
4B
The correct Answer is:d
To solve the problem, we need to analyze the relationship between the magnetic field produced by a circular coil and the parameters involved, specifically the number of turns and the radius of the coil.
1. Understanding the Magnetic Field Formula:
The magnetic field B at the center of a circular coil is given by the formula:
B=μ0NI2R
where:
- μ0 is the permeability of free space,
- N is the number of turns,
- I is the current,
- R is the radius of the coil.
2. Single Turn Coil:
For a single turn coil (where N=1), the magnetic field at the center is:
B=μ0I2R
According to the problem, this magnetic field is given as B.
3. Two Turns Coil:
Now, we take the same length of wire and make two turns. The length of the wire remains the same, but the radius will change.
- The length of wire L can be expressed as:
L=2πR
for the single turn.
- For two turns, the total length of wire used is still L, but now we have:
L=2×2πr′=4πr′
where r′ is the new radius for the two turns.
4. Finding the New Radius:
Since the length of the wire remains constant, we can set the two equations equal:
2πR=4πr′
Simplifying this gives:
R=2r′⇒r′=R2
5. Calculating the New Magnetic Field:
Now substituting N=2 and R=2r′ into the magnetic field formula:
B′=μ0(2)I2r′=μ0(2)I2(R2)=μ0(2)IR
This can be rewritten as:
B′=4(μ0I2R)=4B
6. Conclusion:
Therefore, the magnetic field for two turns of the wire carrying the same current is:
B′=4B
Final Answer:
The value of the magnetic field for two turns of the same wire carrying the same current is 4B.
The magnetic field B at the center of a circular coil is given by the formula:
B=μ0NI2R
where:
- μ0 is the permeability of free space,
- N is the number of turns,
- I is the current,
- R is the radius of the coil.
For a single turn coil (where N=1), the magnetic field at the center is:
B=μ0I2R
According to the problem, this magnetic field is given as B.
Now, we take the same length of wire and make two turns. The length of the wire remains the same, but the radius will change.
L=2πR
for the single turn.
L=2×2πr′=4πr′
where r′ is the new radius for the two turns.
Since the length of the wire remains constant, we can set the two equations equal:
2πR=4πr′
Simplifying this gives:
R=2r′⇒r′=R2
Now substituting N=2 and R=2r′ into the magnetic field formula:
B′=μ0(2)I2r′=μ0(2)I2(R2)=μ0(2)IR
This can be rewritten as:
B′=4(μ0I2R)=4B
Therefore, the magnetic field for two turns of the wire carrying the same current is:
B′=4B
The value of the magnetic field for two turns of the same wire carrying the same current is 4B.
Similar Questions
For a given length l of wire carrying a current l, how many circular turns would produce the maximum magnetic moment ?
View SolutionThe magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is
View SolutionA circular coil of wire carries a current . PQ is a part of very long wire carrying a current and passing close to the circular coil. If the direction of currents are those shown in figure, then the direction of the force acting on PQ is

View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionWhen current is passed through a circular wire prepared from a conducting material, the magnetic field produced at its centre is B. Now a loop having two turns is prepared from the same wire and the same current is passed through it. The magnetic field at its centre will be :
View SolutionThe magnetic field midway between two parallel current carrying wires, carrying currents I and 2i in same direction is B. If the current in the wire with current I is switched off, the magnetic field will become
View SolutionWhen a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to some current flowing is B1 If the same wire is turned into three loops to make a circular coil, the magnetic induction at the center of this coil for the same current will be
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
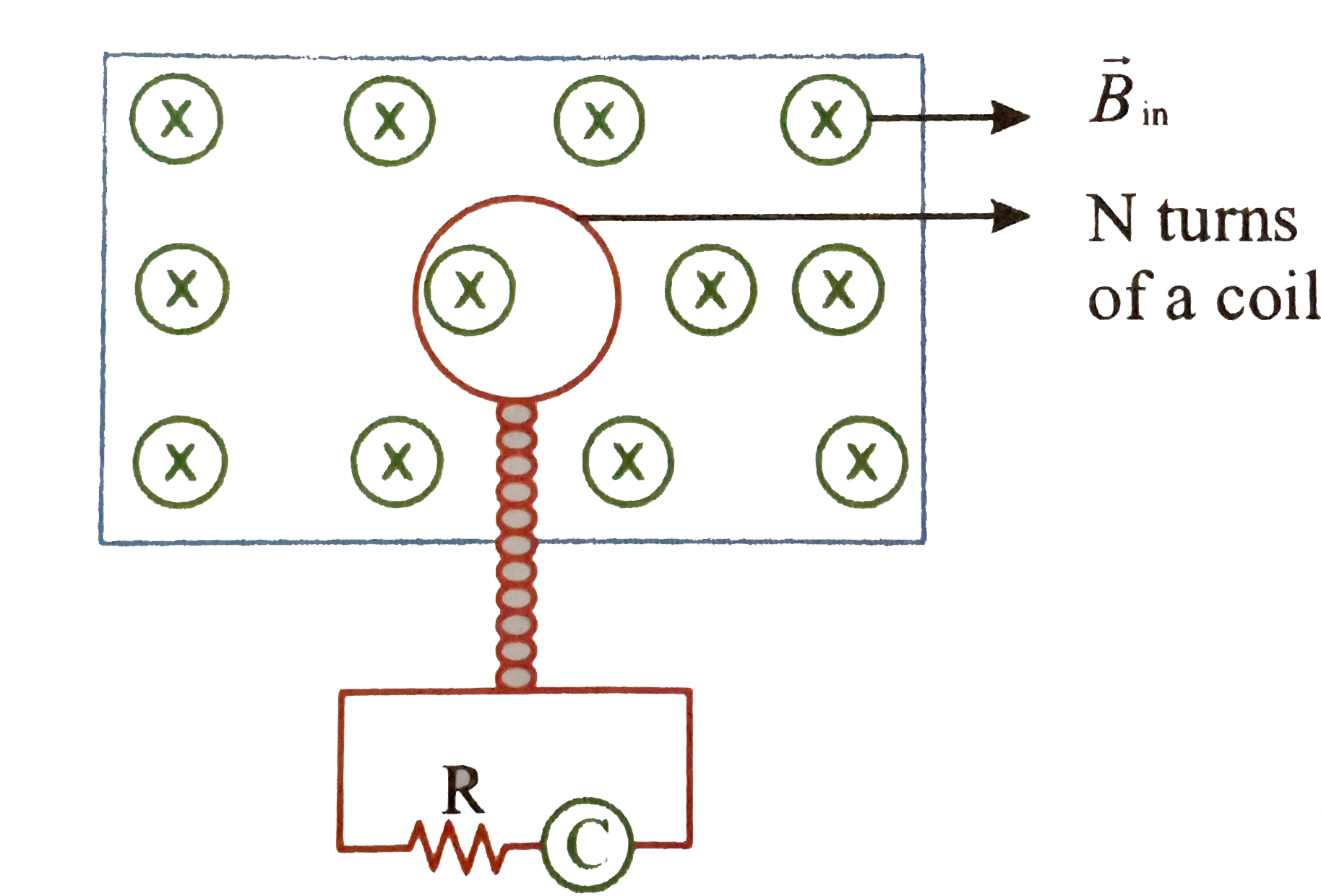
View SolutionA circular coil carrying a certain, current produces a magnetic field B0 at its center. The coil is now rewound so as to have 3 turns and the same currents is passed through it. The new magnetic field at the center is
View SolutionA conductor of length L and carrying current i is bent to form a coil of two turns.Magnetic field at the centre of the coil will be
View Solution
