A bar magnet is oscillating in the earth's magnetic field with a period T. What happens to its period and motion if its mass is quadrupled
Motion remains simple harmonic with new period
Motion remains simple harmonic with new period
Motion remains simple harmonic with new period
Motion remains simple harmonic and the period stays nearly constant
The correct Answer is:B
To solve the problem, we need to analyze how the period of oscillation of a bar magnet changes when its mass is quadrupled. We will use the formula for the period of oscillation of a vibrating magnetometer.
1. Understand the Formula for the Period:
The period T of a bar magnet oscillating in a magnetic field is given by the formula:
T=2π√ImB
where:
- I is the moment of inertia of the magnet,
- m is the mass of the magnet,
- B is the magnetic field strength.
2. Identify the Change in Mass:
The problem states that the mass of the bar magnet is quadrupled. If the original mass is m, the new mass m′ becomes:
m′=4m
3. Substitute the New Mass into the Formula:
We need to find the new period T′ when the mass is quadrupled:
T′=2π√Im′B=2π√I4mB
4. Simplify the Expression:
We can simplify the expression for T′:
T′=2π√I4mB=2π⋅12√ImB=12T
Thus, the new period T′ is half of the original period T.
5. Conclusion about Motion:
The motion of the bar magnet remains simple harmonic because the nature of the oscillation does not change with mass. The only change is in the period of oscillation.
Final Result:
- The new period T′=12T.
- The motion remains simple harmonic.
The period T of a bar magnet oscillating in a magnetic field is given by the formula:
T=2π√ImB
where:
- I is the moment of inertia of the magnet,
- m is the mass of the magnet,
- B is the magnetic field strength.
The problem states that the mass of the bar magnet is quadrupled. If the original mass is m, the new mass m′ becomes:
m′=4m
We need to find the new period T′ when the mass is quadrupled:
T′=2π√Im′B=2π√I4mB
We can simplify the expression for T′:
T′=2π√I4mB=2π⋅12√ImB=12T
Thus, the new period T′ is half of the original period T.
The motion of the bar magnet remains simple harmonic because the nature of the oscillation does not change with mass. The only change is in the period of oscillation.
- The new period T′=12T.
- The motion remains simple harmonic.
Similar Questions
A bar magnet is oscillating in the earth's magnetic field with a time period T. If the mass is increased four times, then its time period will be:
View SolutionTime period of a bar magnet oscillating in earth's magnetic field is T. Its magnetic moment is M. Now, a bar magnet of magnetic moment 2M is brought near it. The new time period will be
View SolutionA bar magnet oscillates in a region of uniform magnetic field with time period T . Now , a piece of wood identical in all respects in terms of mass and length is joined with bar magnet as shown . The new time period of oscillation is
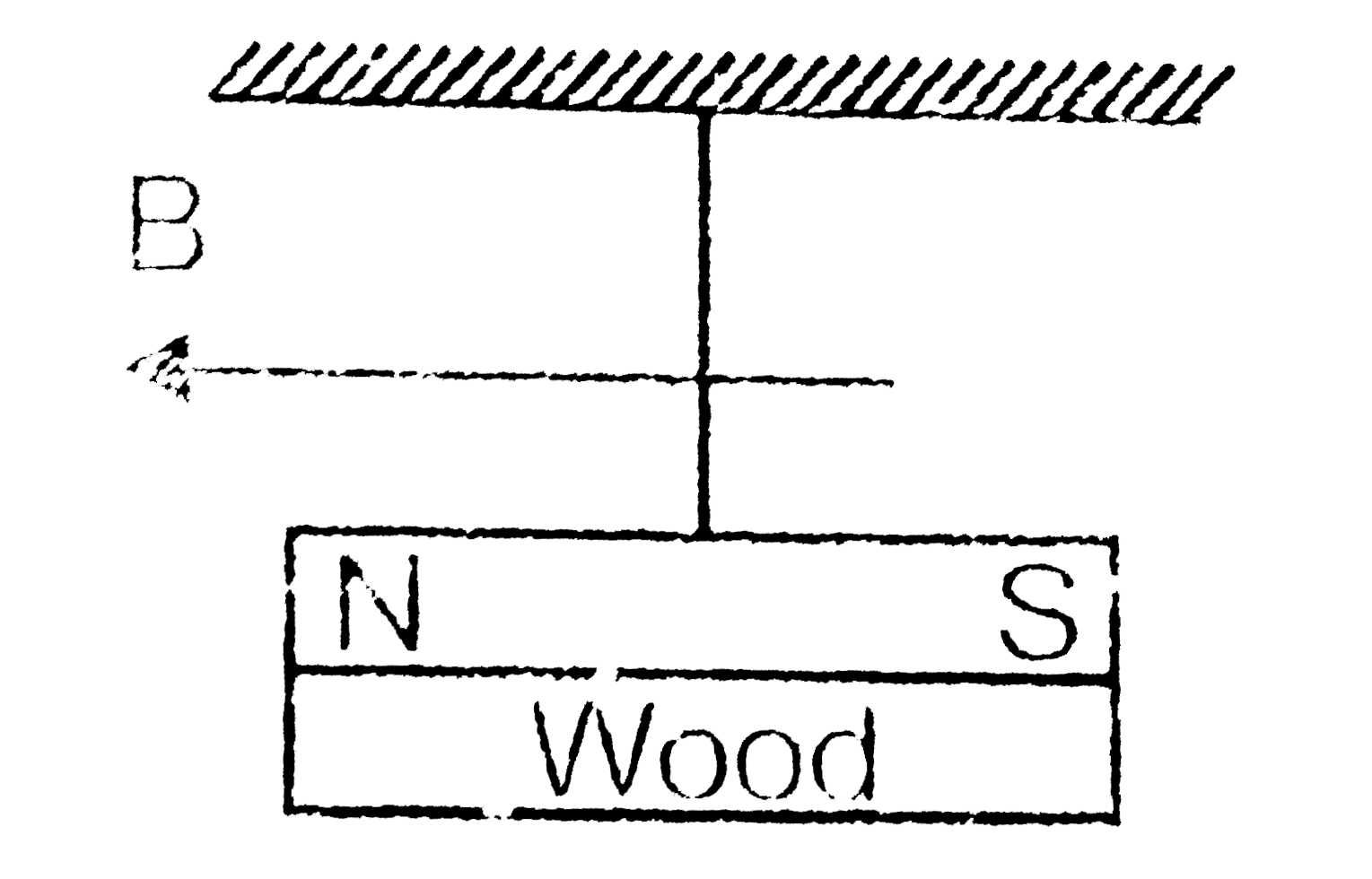 View Solution
View SolutionA magnet is suspended horizontal in the earth's magnetic field. When it is displaced and then released it oscillates in a horizontal plane with a period T. If a place of wood of the same moment of inertia (about the axis of rotation) as the magnet is attached to the magnet what would the new period of oscillation of the system become?
View SolutionThe time period of the magnetic in an oscillation pmagnetometer in the earth magnetic field is 2s. A short bar magnet is placed to the north of the magnetometer, at a separation 10cm from the oscillation magnet, with its north pole pointing towards north. The time period beceomes half. Calculate the magnetic moment of this short magnet.
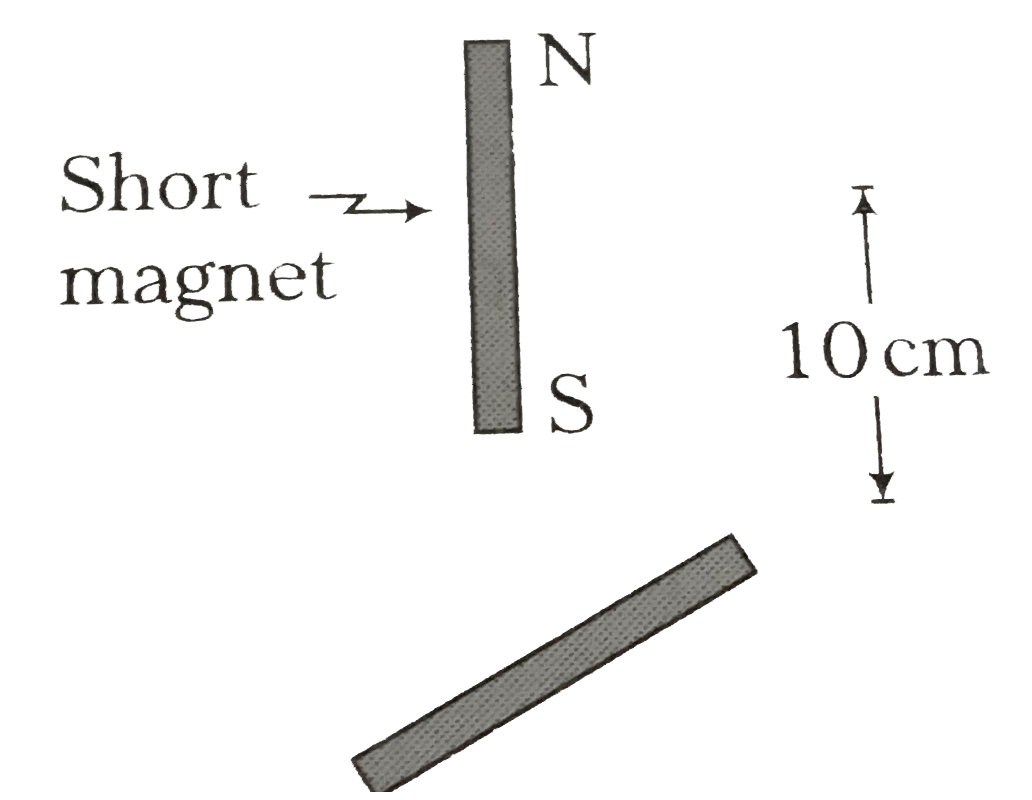 View Solution
View SolutionA small bar magnet A oscillates in a horizontal plane with a period T at a place where the angle of dip is 60∘. When the same needle is made to oscillate in a vertical plane coinciding with the magnetic merdian, its period will be
View SolutionA small magnetic needle performs 10 oscillations/minute in the earth's horizontal magnetic field . When a bar magnet is placed near the small magnet in same position , frequency of oscillations becomes 10√2 oscillations/minute . If the bar magnet be turned around end to end , the rate of oscillation of small magnet will become
View SolutionTwo bar magnets of the same length and breadth but having magnetic moments M and 2M are joined with like poles together and suspended by a string. The time of oscillation of this assembly in a magnetic field of strength B is 3 sec. What will be the period of oscillation, if the polarity of one of the magnets is changed and the combination is again made to oscillate in the same field ?
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View SolutionIf particle is excuting simple harmonic motion with time period T, then the time period of its total mechanical energy is :-
View Solution

