A series R−C circuit is connected to an alternating voltage source. Consider two situations
(a) When capacitor is air filled.
(b) When capacitor is mica filled.
current through resistor is i and voltage across capacitor is V then
Va<Vb
Va>Vb
ia>ib
Va=Vb
The correct Answer is:B
To solve the problem regarding the series R-C circuit connected to an alternating voltage source under two different conditions (air-filled capacitor and mica-filled capacitor), we will follow these steps:
1. Understanding the Circuit:
- We have a series R-C circuit connected to an AC voltage source. The circuit consists of a resistor (R) and a capacitor (C).
2. Capacitive Reactance:
- The capacitive reactance (X_C) is given by the formula:
XC=1ωC
- Where ω is the angular frequency of the AC source and C is the capacitance of the capacitor.
3. Impedance of the Circuit:
- The total impedance (Z) of the R-C circuit is given by:
Z=√R2+X2C
4. Current through the Circuit:
- The current (I) through the circuit can be expressed as:
I=VZ
- Where V is the voltage of the AC source.
5. Case A: Air-Filled Capacitor:
- Let’s denote the current through the air-filled capacitor as IA and the voltage across the capacitor as VA.
- The capacitance CA for an air-filled capacitor is simply C.
- Thus, the capacitive reactance is:
XCA=1ωC
6. Case B: Mica-Filled Capacitor:
- For the mica-filled capacitor, let’s denote the current as IB and the voltage as VB.
- The capacitance CB for a mica-filled capacitor is given by:
CB=K⋅C
- Where K is the dielectric constant of mica (greater than 1).
- Therefore, the new capacitive reactance becomes:
XCB=1ωCB=1ωKC
7. Comparing Impedances:
- Since CB>CA, it follows that XCB<XCA.
- Consequently, the impedance ZB<ZA.
8. Effect on Current:
- Since the impedance decreases in case B, the current increases:
IB>IA
9. Voltage Across the Capacitor:
- The voltage across the capacitor can be expressed as:
V=I⋅XC
- Therefore, for the air-filled capacitor:
VA=IA⋅XCA
- And for the mica-filled capacitor:
VB=IB⋅XCB
10. Conclusion:
- Since IB>IA and XCB<XCA, it follows that:
VB<VA
- Thus, the voltage across the mica-filled capacitor is less than that across the air-filled capacitor:
VB<VA
Final Answer:
The correct conclusion is that the voltage across the mica-filled capacitor (V_B) is less than the voltage across the air-filled capacitor (V_A).
- We have a series R-C circuit connected to an AC voltage source. The circuit consists of a resistor (R) and a capacitor (C).
- The capacitive reactance (X_C) is given by the formula:
XC=1ωC
- Where ω is the angular frequency of the AC source and C is the capacitance of the capacitor.
- The total impedance (Z) of the R-C circuit is given by:
Z=√R2+X2C
- The current (I) through the circuit can be expressed as:
I=VZ
- Where V is the voltage of the AC source.
- Let’s denote the current through the air-filled capacitor as IA and the voltage across the capacitor as VA.
- The capacitance CA for an air-filled capacitor is simply C.
- Thus, the capacitive reactance is:
XCA=1ωC
- For the mica-filled capacitor, let’s denote the current as IB and the voltage as VB.
- The capacitance CB for a mica-filled capacitor is given by:
CB=K⋅C
- Where K is the dielectric constant of mica (greater than 1).
- Therefore, the new capacitive reactance becomes:
XCB=1ωCB=1ωKC
- Since CB>CA, it follows that XCB<XCA.
- Consequently, the impedance ZB<ZA.
- Since the impedance decreases in case B, the current increases:
IB>IA
- The voltage across the capacitor can be expressed as:
V=I⋅XC
- Therefore, for the air-filled capacitor:
VA=IA⋅XCA
- And for the mica-filled capacitor:
VB=IB⋅XCB
- Since IB>IA and XCB<XCA, it follows that:
VB<VA
- Thus, the voltage across the mica-filled capacitor is less than that across the air-filled capacitor:
VB<VA
The correct conclusion is that the voltage across the mica-filled capacitor (V_B) is less than the voltage across the air-filled capacitor (V_A).
Similar Questions
A sereis R-C circuit is connected to AC voltage source. Consider two cases, (A) when C is without a dielectric medium and (B) when C is filled with dielectric of constant 4. The current IR through the resistor and voltage Vc across the capacitor are compared in the two cases. Which of the following is/ are true?
View SolutionAn LCR series circuit is connected to an oscillator (AC supply) having RMS voltage 200 V. If the RMS voltages across resistor, inductor and capacitor are equal, then RMS voltage across the resistor would be
View Solution
Knowledge Check
If a capacitor of 8μF is connected to a 220 V, 100 Hz ac source and the current passing through it is 65 mA, then the rms voltage across it is
A129.4VB12.94VC1.294VD15 V
A 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
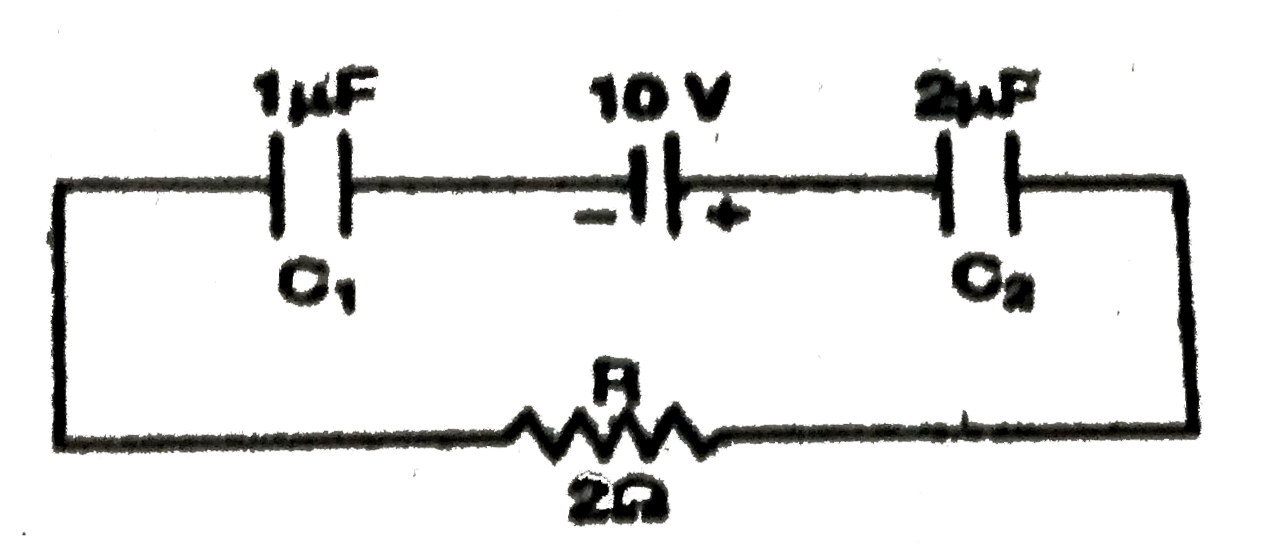
View SolutionAn ac source of 50 V (r.m.s value) is connected across a series R - C circuit. If the r.m.s voltage across the resistor is 40 V, then the r.m.s voltage across the capacitor is
View SolutionEffective capacitance of parallel combination of two capacitors C1andC2 is 10μF. When the capacitors are individually connected to a voltage source of 1V, the energy stored in the capacitor C2 is 4 times of C1. If these capacitors are connected in series, their effective capacitor will be: lt
View SolutionA series L-C-R circuit is connected across a variable frequency source of emf. VL,VC,VR are instantaneous voltage drops across inductor capacitor and resistor and V is instantaneous voltage across the circuit.
Column I Column II(A)|V|(p)Can be greater than zero(B)|V|−|VL|(q)Can be less than zero(C)|V|−|VC|(r)Can be equal to zero(D)|V|−|VR|
View SolutionA 1.00mH inductor and a 1.00μF capacitor are connected in series. The current in the circuit is described by i=20t, where t, is in second and i is in ampere. The capacitor initially has no charge. Determine
(a) the voltage across the inductor as a function of time,
(b) the voltage across the capacitor as a function of time,
(c) the time when the energy stored in the capacitor first exceeds that in the inductor.
View SolutionIn series LCR circuit voltage drop across resistance is 8V, across inductor is 6V and across capacitor is 12V. Then
View SolutionIn a circuit L,C and R are connected in series with an alternating voltage source of frequency f. The current lead the voltages by 45∘. The value of C is :
View Solution
