If the force on a rocket moving with a velocity of 300 m/s is 345 N, then the rate of combustion of the fuel is
(a) 0.55 kg/s
(b) 0.75 kg/s
(c) 1.15 kg/s
(d) 2.25 kg/s
0.55 kg/s
0.75 kg/s
1.15 kg/s
2.25 kg/s
The correct Answer is:C
To solve the problem, we will use the formula related to the force acting on a rocket due to the combustion of fuel. The force (F) on the rocket is given by the equation:
F=Vdmdt
where:
- F is the force,
- V is the velocity of the rocket,
- dmdt is the rate of combustion of the fuel.
Step 1: Identify the given values
From the question, we have:
- Force F=345N
- Velocity V=300m/s
Step 2: Rearrange the formula to find the rate of combustion
We need to find dmdt, so we rearrange the equation:
dmdt=FV
Step 3: Substitute the known values into the equation
Now, substitute the values of force and velocity into the equation:
dmdt=345N300m/s
Step 4: Perform the calculation
Now, calculate the right-hand side:
dmdt=345300
Calculating this gives:
dmdt=1.15kg/s
Step 5: Conclusion
Thus, the rate of combustion of the fuel is:
Answer: dmdt=1.15kg/s
The correct option is (c) 1.15 kg/s.
---
- F is the force,
- V is the velocity of the rocket,
- dmdt is the rate of combustion of the fuel.
From the question, we have:
- Force F=345N
- Velocity V=300m/s
We need to find dmdt, so we rearrange the equation:
Now, substitute the values of force and velocity into the equation:
Now, calculate the right-hand side:
Thus, the rate of combustion of the fuel is:
Similar Questions
Knowledge Check
The force on a rocket moving with a veloctiy 300 m/s is 210N. The rate of consumption of fuel of rocket is
A0.07kgs−1B1.4kgs−1C0.7kgs−1D10.7kgs−1
A 0.5 kg ball moves in a circle of radius 0.4 m at a velocity of 4 m/s. The centripetal force on the ball is
View SolutionA body of mass 5 kg is moving with velocity 2 ms−1. Calculate its linear momentum.
View SolutionA body of mass 5 kg is moving with velocity 2ms−1. Calculate its linear momentum.
View SolutionAn object of mass 15kg is moving with a uniform velocity of 4m/s. what is the kinetic energy possessed by the object ?
View SolutionA rocket of mass 20kg has 180kg fuel. The exhaust velocity of the fuel is 1.6km/s. Calculate the minimum rate of consumption of fuel so that the rocket may rise from the ground. Also, calculate the ultimate vertical speed gained by the rocket when the rate of consumption of fuel is (g=9.8m/s2)
(i) 2kg/s (ii) 20kg/s
View SolutionFigure shows a boy on a horizontal platform A on a smooth horizontal surface, holding a rope attached to a box B. Boy pulls the rope with a constant force of 50 N. The combined mass of platform A and boy is 250kg and that' of box B is 500kg. The velocity of A relative to the box B 5 s after the boy on A begins to pull ,the rope,will be:
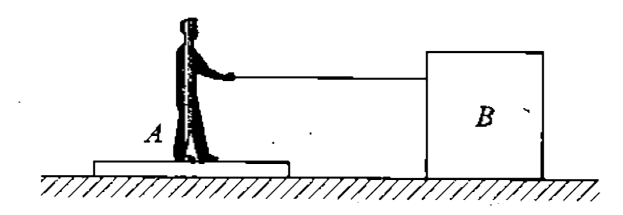 (A)1ms(B)2ms(C)0.5ms(D)1.5ms
(A)1ms(B)2ms(C)0.5ms(D)1.5ms
View SolutionCertain force acting on a 20 kg mass changes its velocity from 5m/s→2m/s. calculate the work done by the force.
View Solution