A 1.5 kg hammer moving with a velocity of 10 m/s strikes a nail for 0.005 s. The average force exerted on the nail is
5000 N
3000 N
1500 N
750 N
The correct Answer is:C
To find the average force exerted on the nail by the hammer, we can use the relationship between momentum, force, and time. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the hammer (m) = 1.5 kg
- Initial velocity of the hammer (v1) = 10 m/s
- Final velocity of the hammer (v2) = 0 m/s (since it comes to rest)
- Time duration (t) = 0.005 s
Step 2: Calculate the change in momentum
The change in momentum (Δp) can be calculated using the formula:
Δp=m(v2−v1)
Substituting the values:
Δp=1.5kg×(0m/s−10m/s)=1.5kg×(−10m/s)=−15kg m/s
Step 3: Relate change in momentum to average force
According to the impulse-momentum theorem:
Δp=Favg×t
Where Favg is the average force. Rearranging the formula gives:
Favg=Δpt
Step 4: Substitute the values to find average force
Substituting the change in momentum and time into the equation:
Favg=−15kg m/s0.005s=−3000N
The negative sign indicates that the force is in the opposite direction of the hammer's initial motion, but we are interested in the magnitude of the force:
Favg=3000N
Conclusion
The average force exerted on the nail is 3000 N.
---
- Mass of the hammer (m) = 1.5 kg
- Initial velocity of the hammer (v1) = 10 m/s
- Final velocity of the hammer (v2) = 0 m/s (since it comes to rest)
- Time duration (t) = 0.005 s
The change in momentum (Δp) can be calculated using the formula:
Δp=m(v2−v1)
Substituting the values:
Δp=1.5kg×(0m/s−10m/s)=1.5kg×(−10m/s)=−15kg m/s
According to the impulse-momentum theorem:
Δp=Favg×t
Where Favg is the average force. Rearranging the formula gives:
Favg=Δpt
Substituting the change in momentum and time into the equation:
Favg=−15kg m/s0.005s=−3000N
The negative sign indicates that the force is in the opposite direction of the hammer's initial motion, but we are interested in the magnitude of the force:
Favg=3000N
The average force exerted on the nail is 3000 N.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH SERIESChapter:LAWS OF MOTIONExercise:EXERCISE - II
Explore 136 Videos
- GEOMETRICAL OPTICSBook:AAKASH SERIESChapter:GEOMETRICAL OPTICSExercise:ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
Explore 10 Videos
- LOGIC GATESBook:AAKASH SERIESChapter:LOGIC GATESExercise:Exercise (Very Short Answer)
Explore 10 Videos
Similar Questions

A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
View SolutionA ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View Solution
Knowledge Check
A body of mass 5 kg is moving with a velocity of 20 m/s. If a force of 100 N is applied on it for 10 s in the same direction as its velocity, what will be the velociy of the body ?
A200 m/sB220 m/sC240 m/sD260 m/sA 3 kg ball strikes a heavy rigid wall with a speed of 10 m/s at an angle of 60∘. It gets reflected with the same speed and angle as shown in Fig. 15.3.11. It the ball is in contact with the wal for 0.20 s, what is the average force exerted on the ball by the wall ?
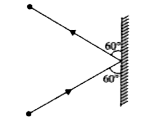 AzeroB150 NC150 √3 ND300 N
AzeroB150 NC150 √3 ND300 N
A ball of mass 0.5kg moving with a velocity of 2m/s strikes a wall normally and bounces back with the same speed . If the time of contact between the ball and the wall is 1 millisecond , the average force exerted by the wall on the ball is
View SolutionA 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted on the bullet will be
View SolutionA 10 g bullet moving at 200 m/s stops after penetrating 5 cm of wooden plank. The average force exerted by the bullet will be
View SolutionA bullet weighing 10 g and moving with a velocity 300 m/s strikes a 5 kg block of ice and drop dead. The ice block is kept on smooth surface. The speed of the block after the the collision is
View SolutionA cricket ball of mass 150 kg is moving with a velocity of 12m/s and is hit by a bat so that ball is turned back with a velocity of 20m/s . The force of the blow acts for 0.01 s on the ball . Find the average force exerted by the bat on the ball.
View SolutionA bullet of mass 50 g moving with an initial velocity 100m s−1 strikes a wooden block and comes to rest after penetrating a distance 2 cm in it. Calculate : Resistive force exerted by the wooden block.
View Solution