A standing wave having 3 nodes and 2 antinodes is formed between two atoms having a distance 1.21Å between them. The wavelength of the standing wave is
1.21 Å
1.42Å
6.05Å
3.63Å
The correct Answer is:a
To find the wavelength of the standing wave formed between two atoms that are 1.21 Å apart, we can follow these steps:
1. Identify the number of nodes and antinodes:
- The problem states that there are 3 nodes and 2 antinodes in the standing wave.
2. Understand the relationship between nodes, antinodes, and wavelength:
- In a standing wave, the distance between two consecutive nodes (or two consecutive antinodes) is half of the wavelength (λ).
- The relationship can be summarized as follows:
- The distance between two nodes = λ/2
- The distance between two antinodes = λ/2
3. Determine the total distance covered by the nodes and antinodes:
- For 3 nodes, there are 2 segments of λ/2 between them.
- Therefore, the total distance (d) between the first node and the last node can be expressed as:
d=(number of segments)×(λ2)
- Since there are 3 nodes, there are 2 segments:
d=2×(λ2)=λ
4. Set the total distance equal to the distance between the atoms:
- The problem states that the distance between the two atoms is 1.21 Å.
- Therefore, we can set up the equation:
λ=1.21Å
5. Conclusion:
- The wavelength of the standing wave is:
λ=1.21Å
Final Answer:
The wavelength of the standing wave is 1.21 Å.
---
- The problem states that there are 3 nodes and 2 antinodes in the standing wave.
- In a standing wave, the distance between two consecutive nodes (or two consecutive antinodes) is half of the wavelength (λ).
- The relationship can be summarized as follows:
- The distance between two nodes = λ/2
- The distance between two antinodes = λ/2
- For 3 nodes, there are 2 segments of λ/2 between them.
- Therefore, the total distance (d) between the first node and the last node can be expressed as:
d=(number of segments)×(λ2)
- Since there are 3 nodes, there are 2 segments:
d=2×(λ2)=λ
- The problem states that the distance between the two atoms is 1.21 Å.
- Therefore, we can set up the equation:
λ=1.21Å
- The wavelength of the standing wave is:
λ=1.21Å
The wavelength of the standing wave is 1.21 Å.
Similar Questions
In a standing wave 4 nodes and 3 antinodes are formed between two fixed end of string of length 6 m.Then the wave length of the standing wave is
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
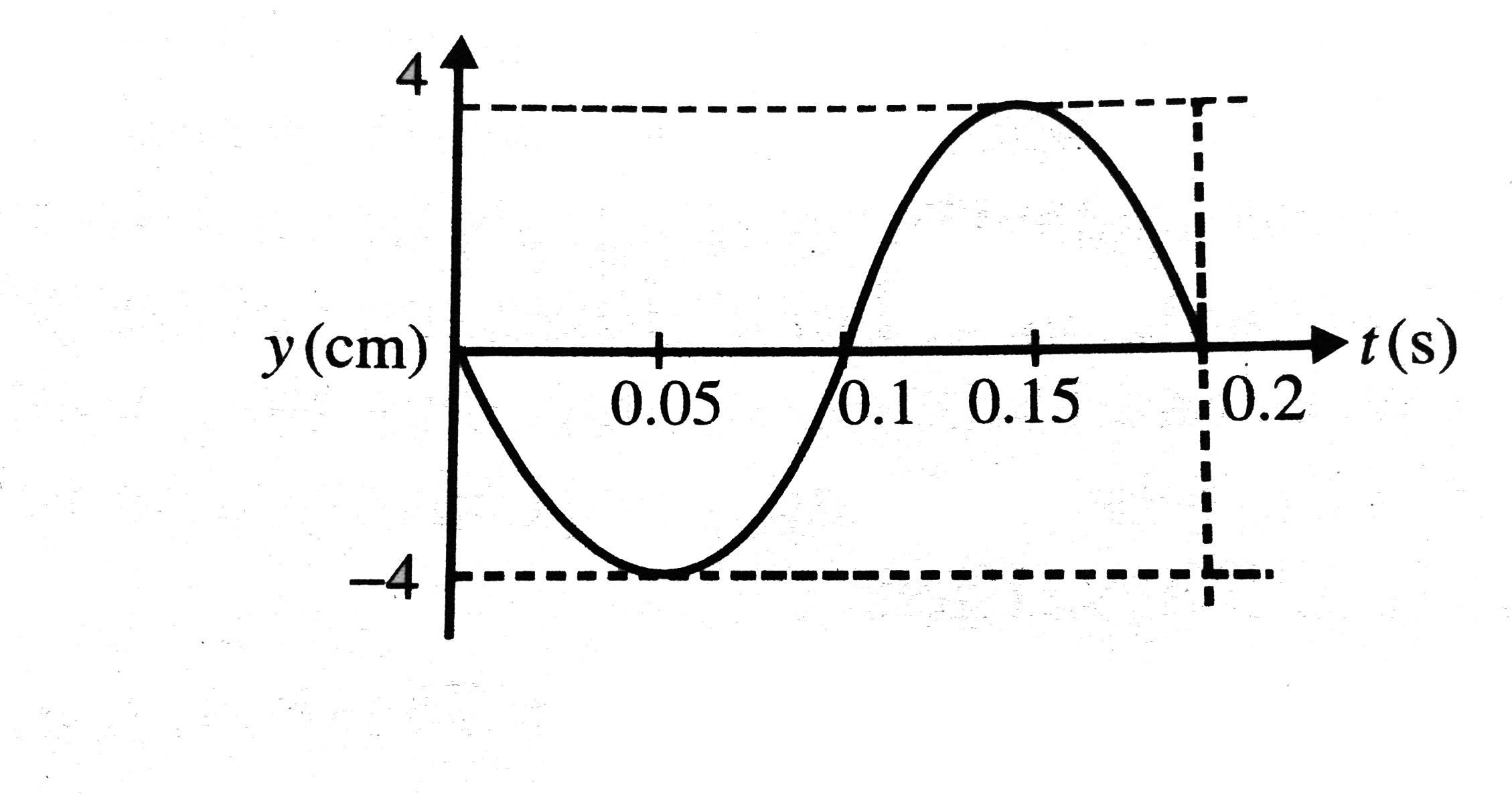
View SolutionFor a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
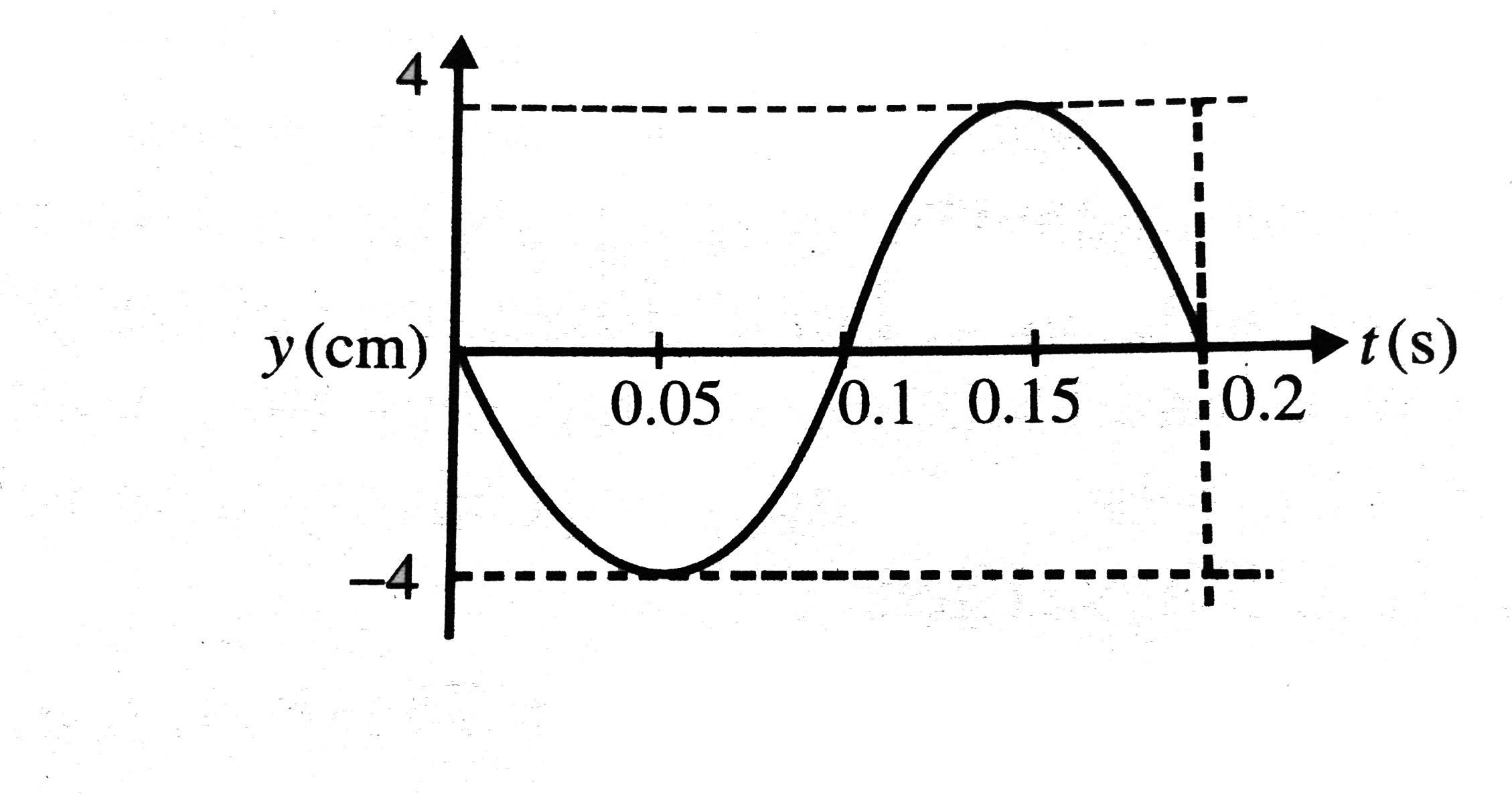
View SolutionA string fixed at both ends has consecutive standing wave modes for which the distances between adjacent nodes are 18 cmand16 cm respectively. The minimum possible length of the string is:
View SolutionThe system of two rods shown in figure is vibrating at the same frequency and forming a standing wave. The ratio of the number of antinodes in the two rods if radius of rod B is twice radius of A and the material and the lengths of the two rods is same : (A)2:1 (B)3:1 (C)2:3 (D)4:1
View SolutionA standing wave in second overtone is maintained in a open pipe of length L. The distance between consecutive displacement node and pressure node is L/x. Find x
View SolutionIn a standing wave the phase difference between two points on either side of a a node will be
View SolutionOcean waves of time period 10 s have wave velocity 15 ms−1. Find the wavelength of these waves .
View SolutionLet us assume that the de-Broglie wave asssociated with an electron froms a standing wave between the atoms arranged in a one-dimensional array with nodes at each of the atomic sites. If is found that one such standing wave is formed, if the distance between the atoms of the array is 3Å. A similar standing wave is again formed, if d is increased to 3.5Å but not for any intermediate value of d. Find the energy of the electrons in electron volts and the least value of d for which the standing wave of the type described above can from.
View SolutionAssume that the de Broglie wave associated with an electron can from a standing wave between the atom arrange in a one dimensional array with nodes at each of the atomic sites. It is found that one such standing wave if the distance d between the atoms of the array is 2A0 A similar standing wave is again formed if d is increased to 2.5Å . Find the energy of the electrons in electron volts and the least value of d for which the standing wave type described above can from .
View Solution
