The system of two rods shown in figure is vibrating at the same frequency and forming a standing wave. The ratio of the number of antinodes in the two rods if radius of rod B is twice radius of A and the material and the lengths of the two rods is same : (A)2:1 (B)3:1 (C)2:3 (D)4:1
To solve the problem of finding the ratio of the number of antinodes in two rods A and B, we can follow these steps:
1. Understanding the Problem: We have two rods, A and B, vibrating at the same frequency and forming standing waves. The radius of rod B is twice that of rod A, and both rods are made of the same material and have the same length.
2. Area Calculation: The area A of a rod is given by the formula:
A=πr2
For rod A with radius r:
AA=πr2
For rod B with radius 2r:
AB=π(2r)2=4πr2
Thus, the area of rod B is 4 times that of rod A:
AB=4AA
3. Frequency Relation: The frequency of vibration for a rod can be expressed as:
f=n12√Tμ
where n is the number of loops (or antinodes), T is the tension, and μ is the mass per unit length.
4. Mass per Unit Length: The mass per unit length μ can be expressed in terms of density ρ and area A:
μ=ρ⋅A
Therefore, for rods A and B:
μA=ρ⋅AAandμB=ρ⋅AB=ρ⋅4AA
5. Setting Up the Frequency Equations: Since both rods are vibrating at the same frequency:
nA12√TμA=nB12√TμB
Cancelling 12 and T from both sides gives:
nA√1μA=nB√1μB
6. Substituting for Mass per Unit Length:
nA√1ρAA=nB√1ρ⋅4AA
The density ρ and area AA cancel out:
nA√11=nB√14
Simplifying gives:
nA=nB⋅12
or
nBnA=2
7. Conclusion: The ratio of the number of antinodes in rods B to A is:
nBnA=2:1
Final Answer:
The ratio of the number of antinodes in the two rods is 2:1, which corresponds to option (A).
A=πr2
For rod A with radius r:
AA=πr2
For rod B with radius 2r:
AB=π(2r)2=4πr2
Thus, the area of rod B is 4 times that of rod A:
AB=4AA
f=n12√Tμ
where n is the number of loops (or antinodes), T is the tension, and μ is the mass per unit length.
μ=ρ⋅A
Therefore, for rods A and B:
μA=ρ⋅AAandμB=ρ⋅AB=ρ⋅4AA
nA12√TμA=nB12√TμB
Cancelling 12 and T from both sides gives:
nA√1μA=nB√1μB
nA√1ρAA=nB√1ρ⋅4AA
The density ρ and area AA cancel out:
nA√11=nB√14
Simplifying gives:
nA=nB⋅12
or
nBnA=2
nBnA=2:1
The ratio of the number of antinodes in the two rods is 2:1, which corresponds to option (A).
Similar Questions
Four rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
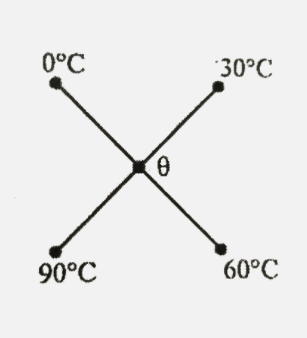
View SolutionRatio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
View Solution
Knowledge Check
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity VA/VB is
A2B√2C1/√2D1/2
Figure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are

View SolutionFigure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are

View SolutionTwo ends of rods of length L and radius R of the same material of kept at the same temperature. Which of the following rods conducts the maximum heat?
View SolutionThe ratio of thermal conductivity of two rods of different material is 5:4. The two rods of same area of cross-section and same thermal resistance will have the lengths in the ratio
View SolutionThe ratio of the thermal conductivities of two different materials is 1:2. The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View SolutionThe y co - ordinate of the centre of mass of the system of three rods of length 2a and two rods of length a as shown in the figure is (Assume all rods to be of uniform density)
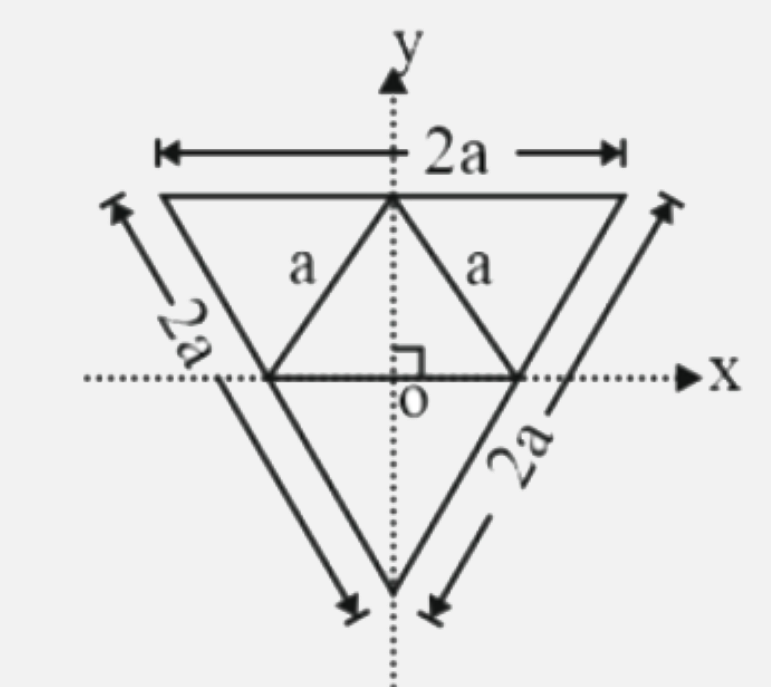
View SolutionThree rods of equal length of same material are joined to form an equilateral triangle ABC as shown in figure. Area of cross-section of rod AB is S, of rod BC is 2S and that of AC is S. Then match the following.

View Solution
