In a sinusoidal wave the time required for a particular point to move from equilibrium position to maximum displacement is 0.17s, then the frequency of wave is:
1.47 Hz
0.36 Hz
0.73 Hz
2.94 Hz
The correct Answer is:a
To solve the problem, we need to find the frequency of the wave given the time taken for a point on the wave to move from the equilibrium position to maximum displacement.
1. Understand the Motion: In a sinusoidal wave, the motion of a particle can be described as simple harmonic motion (SHM). The equilibrium position is the mean position, and the maximum displacement is the extreme position.
2. Identify the Time Interval: The problem states that the time required for a particle to move from the equilibrium position to maximum displacement is 0.17s.
3. Relate Time to Period: In SHM, the time taken to move from the mean position (equilibrium) to the extreme position (maximum displacement) is one-fourth of the total time period T of the wave. This can be expressed as:
T4=0.17s
4. Calculate the Period T: To find the total period T, we can rearrange the equation:
T=4×0.17s=0.68s
5. Calculate the Frequency f: The frequency f is the reciprocal of the period T:
f=1T=10.68s≈1.47Hz
Final Answer:
The frequency of the wave is approximately 1.47Hz.
---
T4=0.17s
T=4×0.17s=0.68s
f=1T=10.68s≈1.47Hz
The frequency of the wave is approximately 1.47Hz.
Similar Questions
Knowledge Check
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.17 sec. The frequency of the wave is
A1.47 HzB0.36 HzC0.73 HzD2.94 Hz
Time period of a wave is 5×10−3s, what is the frequency?
View SolutionA string fixed at both ends, is vibrating in a particular mode of vibration. Vibration is such that a point on string is at maximum displacement and it is at a distance of one fourth of length of string from one end. The frequency of vibration in thus mode is 200Hz. What will be the frequency of vibration when it vibrates in next mode such that the same point is at maximum displacement?
View SolutionA body of mass 0.10kg is attached to vertical massless spring with force constant 4.0×103N/m. The body is displaced 10.0cm from its equilibrium position and released. How much time elapses as the body moves from a point 8.0cm on one side of the equilibrium position to a point 6.0cm on the same side of the equilibrium position ?
View SolutionTime period of a back performing SHM is 2 second and it can travel to and fro from equilibrium position upto maximum 5cm. At start the pendulum is at maximum displacement on right side of equilibrium position. Find displacement and time relation.
View SolutionA source of wave produces 40 crests and 40 troughs in 0.4 s. What is the frequency of the wave ?
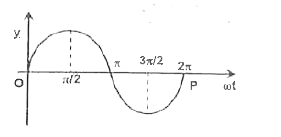
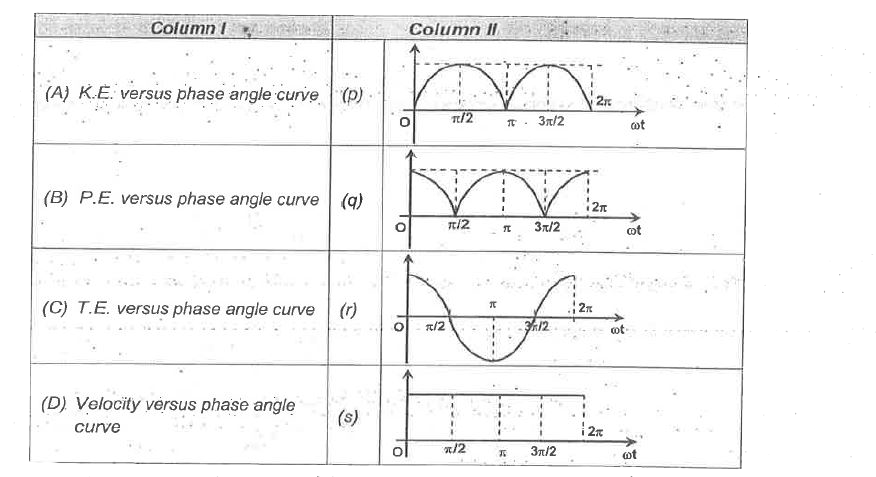
View SolutionThe graph plotted between phase angle (ωt) and displacement of a particle from equilibrium position (y) is a sinusoidal curve as shown below. Then the best matching is
View SolutionFrom a wave equation
y=0.5sin(2π3.2)(64t−x).
the frequency of the wave is
View Solution
