In a sinusoidal wave, the time required by a particular particle to move from maximum displacement to zero displacement is 0.025 sec. The frequency of the wave is
2.5 Hz
5 Hz
7.5 Hz
10 Hz
The correct Answer is:D
To find the frequency of the sinusoidal wave given the time it takes for a particle to move from maximum displacement to zero displacement, we can follow these steps:
1. Understand the Motion of the Particle:
- In a sinusoidal wave, a particle moves from maximum displacement (amplitude) to zero displacement (equilibrium position). This motion corresponds to a quarter of a complete cycle of the wave.
2. Identify the Time Given:
- The time taken for the particle to move from maximum displacement to zero displacement is given as t=0.025 seconds.
3. Relate Time to the Wave Period:
- Since moving from maximum displacement to zero displacement represents a quarter of the wave's period T, we can express this relationship mathematically:
t=T4
4. Calculate the Wave Period T:
- Rearranging the equation gives:
T=4t=4×0.025s=0.1s
5. Calculate the Frequency f:
- Frequency f is the reciprocal of the period T:
f=1T=10.1s=10Hz
Final Answer:
The frequency of the wave is 10Hz.
---
- In a sinusoidal wave, a particle moves from maximum displacement (amplitude) to zero displacement (equilibrium position). This motion corresponds to a quarter of a complete cycle of the wave.
- The time taken for the particle to move from maximum displacement to zero displacement is given as t=0.025 seconds.
- Since moving from maximum displacement to zero displacement represents a quarter of the wave's period T, we can express this relationship mathematically:
t=T4
- Rearranging the equation gives:
T=4t=4×0.025s=0.1s
- Frequency f is the reciprocal of the period T:
f=1T=10.1s=10Hz
The frequency of the wave is 10Hz.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 second. The frequency of the wave is
A1.47 HzB0.36 HzC0.73 HzD2.94 HzIn a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 second. The frequency of the wave is
A0.73 HzB0.36 HzC1.47 HzD2.94 HzIn a sinusoidal wave the time required for a particular point to moce from equilibrium pasition to maximum diaplacement is 0.17s, then the frequency of wave is:
A1.47HzB0.36HzC2.94HzD2.48Hz
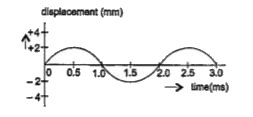
The figure shows displacement time graph of a wave. The frequency of this wave is displacement (mm)
View SolutionWhen a sound wave of frequency 200 Hz travels through a medium, the maximum displacement of a particle of the medium is 0.2 cm. The maximum velocity of the particle is
View SolutionWhen a sound wave of frequency 300 Hz passes through a medium the maximum displacement of a particle of the medium is 0.1 cm . The maximum velocity of the particle is equal to
View SolutionThe distance between maximum and the next minimum displacement in a wave is 6cm. The wavelength of the wave is :
View SolutionThe figure shows a velocity-time graph of a particle moving along a straight line
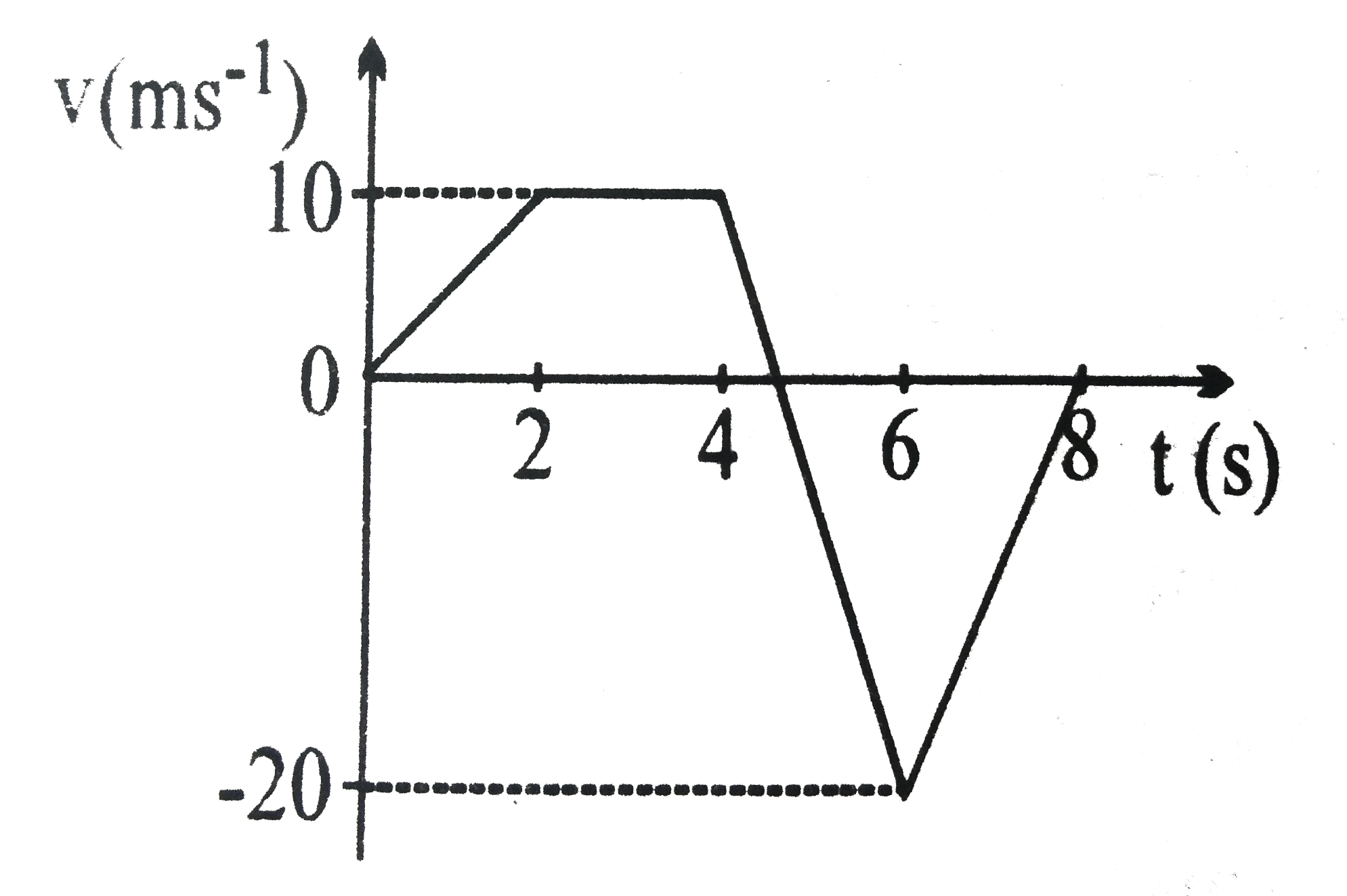
The maximum displacement of the particle is
View Solution