Young's double slit experiment is first performed in air and then in a medium other than air. It is found than 8th bright fringe in the medium lies where 5th daek fringe lies in air. The re3fractive index of the medium is nearly
1.25
1.59
1.69
1.78
The correct Answer is:D
To solve the problem, we need to analyze the conditions of Young's double slit experiment in both air and another medium.
1. Understanding the Problem:
- We have two scenarios: one in air and the other in a medium with a refractive index μ.
- The 8th bright fringe in the medium corresponds to the position of the 5th dark fringe in air.
2. Path Difference for Bright and Dark Fringes:
- For the 8th bright fringe in the medium, the path difference is given by:
Path difference=8λ(where λ is the wavelength in the medium)
- For the 5th dark fringe in air, the path difference is given by:
Path difference=(2n−1)λ02=9λ02(where λ0 is the wavelength in air)
3. Equating the Path Differences:
- Since both fringes occur at the same position, we can set the two path differences equal to each other:
8λ=9λ02
4. Expressing Wavelengths:
- Rearranging the equation gives:
16λ=9λ0
- Thus, we can express the ratio of the wavelengths:
λ0λ=169
5. Finding the Refractive Index:
- The refractive index μ of the medium is given by the ratio of the wavelengths:
μ=λ0λ=169
6. Final Calculation:
- Calculating the numerical value gives:
μ≈1.78
Conclusion:
The refractive index of the medium is nearly 1.78.
- We have two scenarios: one in air and the other in a medium with a refractive index μ.
- The 8th bright fringe in the medium corresponds to the position of the 5th dark fringe in air.
- For the 8th bright fringe in the medium, the path difference is given by:
Path difference=8λ(where λ is the wavelength in the medium)
- For the 5th dark fringe in air, the path difference is given by:
Path difference=(2n−1)λ02=9λ02(where λ0 is the wavelength in air)
- Since both fringes occur at the same position, we can set the two path differences equal to each other:
8λ=9λ02
- Rearranging the equation gives:
16λ=9λ0
- Thus, we can express the ratio of the wavelengths:
λ0λ=169
- The refractive index μ of the medium is given by the ratio of the wavelengths:
μ=λ0λ=169
- Calculating the numerical value gives:
μ≈1.78
The refractive index of the medium is nearly 1.78.
Similar Questions
Young's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View SolutionYoung's double slit experiment is made in a liquid. The tenth bright fringe in liquid lies in screen where 6th dark fringe lies in vacuum. The refractive index of the liquid is approximately
View Solution
Knowledge Check
In Young's double-slit experiment, the slit are 0.5 mm apart and the interference is observed on a screen at a distance of 100 cm from the slits, It is found that the ninth bright fringe is at a distance of 7.5 mm from the second dark fringe from the center of the fringe pattern. The wavelength of the light used in nm is
A25007B2500C5000D50007
In Young.s double slit experiment, what is the path difference between the two light waves forming 5th bright band (fringe) on the screen ?
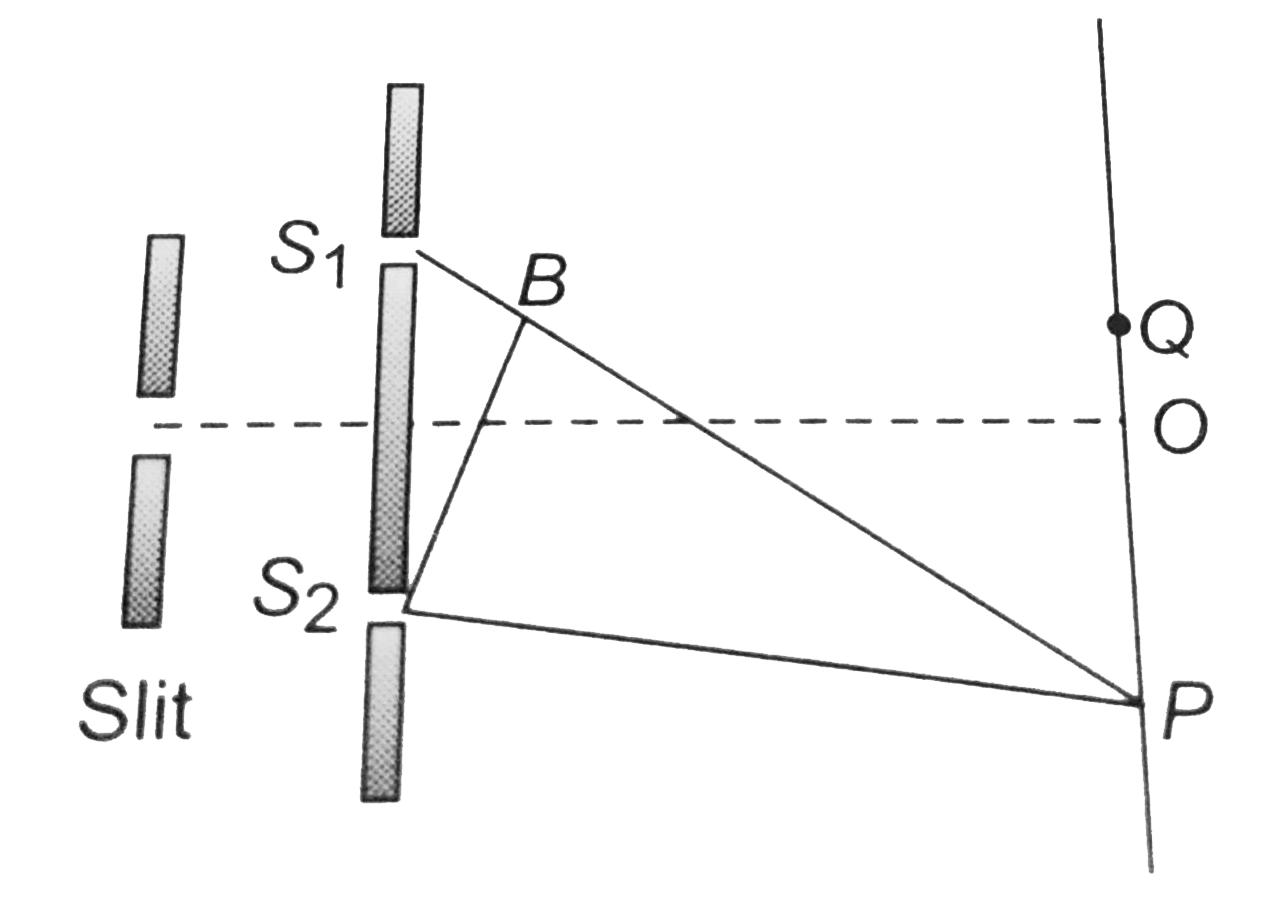
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the 11th bright fringe on the other side, as measured from Q. If the wavelength of the light used is 600nm. Then S1B will be equal to
View SolutionIf white light is used in Young's double -slit experiment
a) bright white fringe is formed at the centre of the screen
b) fringes of different colours are observed on both sides of central fringe clearly only in the first order
c) the first order violet fringes are closer to the centre of the screen than the first order red fringes
d) the first order red fringes are closer to the centre of the screen than the first order violet fringes
View SolutionOn placing a thin film of mica of thickness 12×10−5cm in the path of one of the interfering beams in young's double slit experiment using monochromatic light, the fringe pattern shifts through a distance equal to the width of a bright fringe. If λ=6×10−5cm, the refractive index of mica is
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View SolutionYoung's double slit experiment is perfor-med inside water (μ=43) with light of frequency 6×1014 Hz. If the slits are separated by 0.2 mm and the screen kept 1 m from the slits, find the fringe width. Using the same set-up, what will the fringe width be if the experiment is performed in air?
View SolutionIn a Young's double slit experiment, a parallel beam containing wavelengths λ1=4000Å and λ2=5600Å is incident at an angle ϕ=30∘ on a diaphragm having narrow slits at separation d=2mm. The screen is placed at a distance D =40 cm from the slits. a mica slab of thickness t=5mm is placed in front of one of the slits and whole of the apparatus is submerged in water. if the central bright fringe is observed at C, determine.

(i) The refractive index of the slab
(ii) The distance of first black line from C
both wavelength are in air. take μw=43
View Solution
