A man is 6 ft tall In order to see his entire image, he requires a plane mirror of minimum length equal to
(a)
(b)
(c)
(d)
The correct Answer is:B
To determine the minimum length of a plane mirror required for a 6 ft tall man to see his entire image, we can follow these steps:
1. Understanding the Problem: We need to find the minimum length of a plane mirror that allows a 6 ft tall man to see his entire reflection.
2. Using the Formula: The minimum length of a plane mirror required to see the full image of a person is given by the formula:
Length of mirror=Height of person2
3. Substituting the Height: In this case, the height of the man is 6 ft. We substitute this value into the formula:
Length of mirror=6 ft2
4. Calculating the Length: Now, we perform the division:
Length of mirror=3 ft
5. Conclusion: Therefore, the minimum length of the plane mirror required for the man to see his entire image is 3 ft.
Final Answer:
The correct option is (d) 3 ft.
---
Length of mirror=Height of person2
Length of mirror=6 ft2
Length of mirror=3 ft
The correct option is (d) 3 ft.
Similar Questions
A man of height 6 ft wants to see his full image in a plane mirror. The minimum length of the plane mirror required
View SolutionA man of length h requires a mirror of length at least equal to, to see his own complete image
View SolutionA man is 180 cm tall and his eyes are 10 cm below the top of his head. In order to see his entire height right from tow to head, he uses a plane mirror kept at a distance of 1 m from him. The minimum height of the plane mirror required is
View SolutionIf 5:4::30:x, then the value of x is
(a) 24
(b) 12
(c) 32
(d) 6
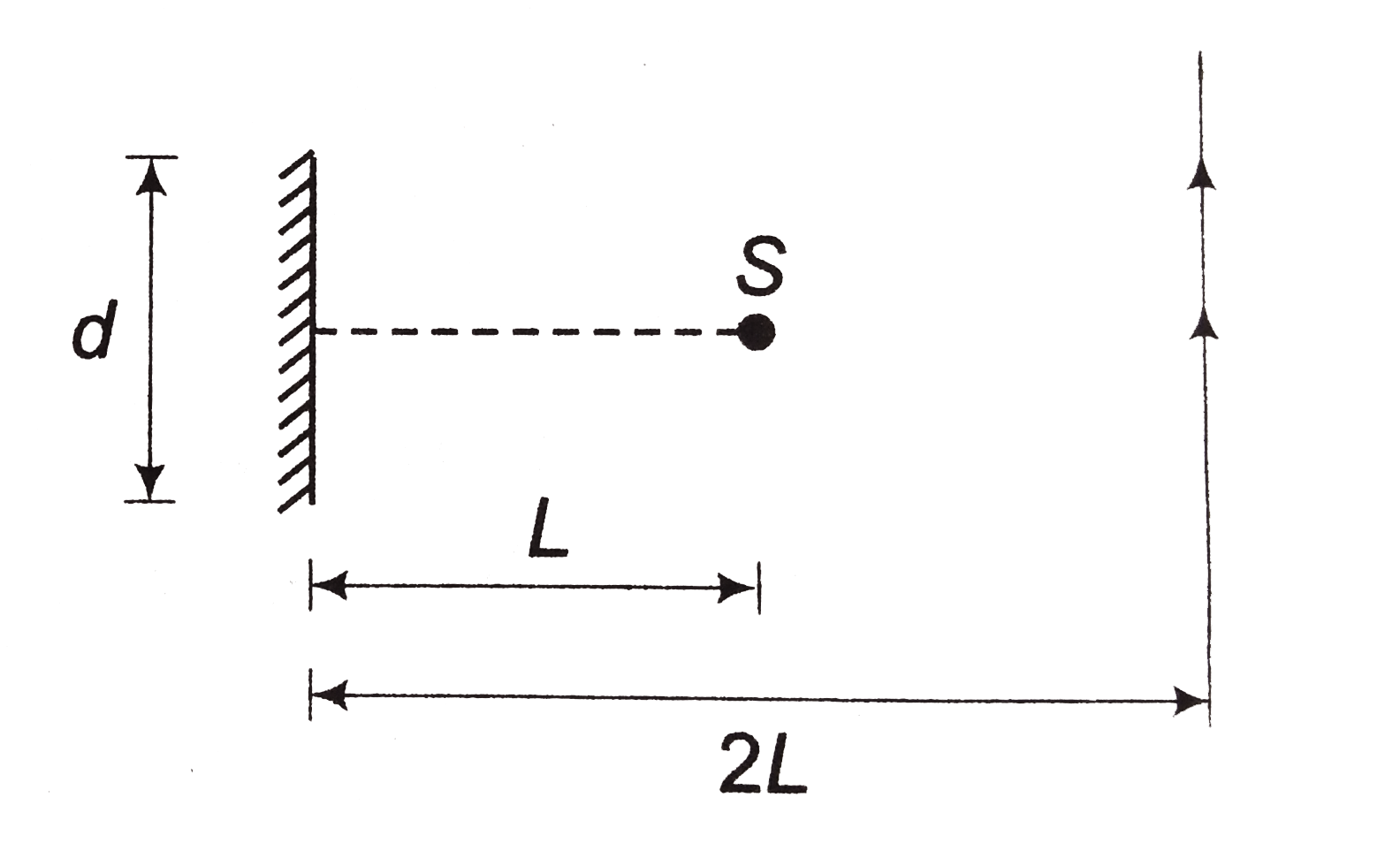
View SolutionA point source of light S, placed at a
distance L in front of the centre of a mirror of width d,
hangs vertically on a wall. A man walks in front of the
mirror along a line parallel to th mirror at a distane
2L form it as shown.The greatest distance over which
he can see the image of the light source in the mirror is
(a) d/2 (b) d (c) 2d (d) 3 d.
View SolutionA point source of light S, placed at a
distance L in front of the centre of a mirror of width d,
hangs vertically on a wall. A man walks in front of the
mirror along a line parallel to th mirror at a distane
2L form it as shown.The greatest distance over which
he can see the image of the light source in the mirror is
(a) d/2 (b) d (c) 2d (d) 3 d.

View SolutionIf a,b,c are the sides of a triangle, then the minimum value of ab+c−a+bc+a−b+ca+b−c is equal to (a)3 (b)6 (c)9 (d)12
View SolutionWhat should be multiplied to 6−2 so that the product may be equal to 216?
(a)64
(b) 65
(c)63
(d) 6
View SolutionA person 1.6 m tall is standing at the center between two walls three meter high. What is the minimum size of a plane mirror fixed on the wall in front of him, if he is to see the full height of the wall behind him?
View Solution(−2)× (−3)× 6 × (−1) is equal to
(a)36
(b) −36
(c) 6
(d) −6
View Solution
