A person 1.6 m tall is standing at the center between two walls three meter high. What is the minimum size of a plane mirror fixed on the wall in front of him, if he is to see the full height of the wall behind him?
0.8 m
1 m
1.5 m
2.3 m
The correct Answer is:B
To determine the minimum size of a plane mirror fixed on the wall in front of a person who is 1.6 m tall and standing at the center between two walls that are 3 m high, we can follow these steps:
Step 1: Understand the Geometry
The person is standing in the middle of a room with two walls, each 3 m high. To see the full height of the wall behind him, the rays of light from the top and bottom of the wall must reflect off the mirror and reach the person's eyes.
Step 2: Define the Variables
Let:
- Height of the person (h) = 1.6 m
- Height of the wall (H) = 3 m
- Height of the mirror (M) = ?
Step 3: Determine the Required Reflection
To see the top of the wall, the light ray from the top of the wall (3 m) must reflect off the mirror and reach the person's eyes. Similarly, to see the bottom of the wall, the light ray from the bottom of the wall (0 m) must also reflect off the mirror.
Step 4: Analyze the Reflection
The height of the mirror needs to be positioned such that:
- The top ray from the wall (3 m) reflects down to the person's eyes.
- The bottom ray from the wall (0 m) reflects up to the person's eyes.
Step 5: Use Similar Triangles
Using the concept of similar triangles:
- The height of the mirror can be split into two segments: A (from the bottom of the mirror to the eye level of the person) and B (from the eye level to the top of the mirror).
- The height of the mirror (M) can be expressed as M = A + B.
Step 6: Establish Relationships
From the geometry:
- The distance from the person to the mirror is equal on both sides since he is in the center.
- The distances can be expressed as:
- A = (Height of the wall - Height of the person) / 2
- B = (Height of the wall - Height of the person) / 2
Step 7: Calculate the Height of the Mirror
Since the total height of the wall is 3 m and the height of the person is 1.6 m:
- A + B = (3 m - 1.6 m) / 2 + (3 m - 1.6 m) / 2
- A + B = (1.4 m) / 2 + (1.4 m) / 2 = 1.4 m
Thus, the minimum height of the mirror (M) required is:
- M = A + B = 1.4 m
Step 8: Conclusion
The minimum size of the plane mirror fixed on the wall in front of the person must be 1 m.
The person is standing in the middle of a room with two walls, each 3 m high. To see the full height of the wall behind him, the rays of light from the top and bottom of the wall must reflect off the mirror and reach the person's eyes.
Let:
- Height of the person (h) = 1.6 m
- Height of the wall (H) = 3 m
- Height of the mirror (M) = ?
To see the top of the wall, the light ray from the top of the wall (3 m) must reflect off the mirror and reach the person's eyes. Similarly, to see the bottom of the wall, the light ray from the bottom of the wall (0 m) must also reflect off the mirror.
The height of the mirror needs to be positioned such that:
- The top ray from the wall (3 m) reflects down to the person's eyes.
- The bottom ray from the wall (0 m) reflects up to the person's eyes.
Using the concept of similar triangles:
- The height of the mirror can be split into two segments: A (from the bottom of the mirror to the eye level of the person) and B (from the eye level to the top of the mirror).
- The height of the mirror (M) can be expressed as M = A + B.
From the geometry:
- The distance from the person to the mirror is equal on both sides since he is in the center.
- The distances can be expressed as:
- A = (Height of the wall - Height of the person) / 2
- B = (Height of the wall - Height of the person) / 2
Since the total height of the wall is 3 m and the height of the person is 1.6 m:
- A + B = (3 m - 1.6 m) / 2 + (3 m - 1.6 m) / 2
- A + B = (1.4 m) / 2 + (1.4 m) / 2 = 1.4 m
- M = A + B = 1.4 m
The minimum size of the plane mirror fixed on the wall in front of the person must be 1 m.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - B)
35 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSIGNMENT (SECTION - C)
80 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - EXERCISE
45 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
- SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS (MATERIAL, DEVICES AND SIMPLE CIRUITS )EXERCISE - Assignment SECTION - D (Assertion & reason type Question)
10 Videos
Similar Questions
A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its vertical axis. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA 70kg man stands in contact against the inner wall of a hollw cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing nis 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View Solution
Knowledge Check
The driver of a car travelling at velocity v suddenly see a broad wall in front of him at a distance d. He should
Abreak sharplyBturn sharplyCboth (a) and (b)Dnone of theseA man stands symmetrically between two large plane mirrors fixed to two adjacent walls of a reactangular room. The number of images formed as
A4B3C2D6
A 70kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3m rotating about its verticle axis. The coefficient of friction between the wall and his clothing is 0.15 . What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed?
View SolutionA man is 180 cm tall and his eyes are 10 cm below the top of his head. In order to see his entire height right from tow to head, he uses a plane mirror kept at a distance of 1 m from him. The minimum height of the plane mirror required is
View SolutionAn optician while testing the eyes of a patient keeps a charge of letters 3 m behind the patient and asks him to see the letters on the image of chart formed in plane mirror kept at distance 2 m in front of him. At what distance is the chart seen by the patient?
View SolutionA 70 kg man stands in contact against the wall of a cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionA person wants to see AB part of his image. His eye level is at 1.8m above the ground. If he uses minimum size of mirror required for this, find the height of the lowest point of mirror above the ground.
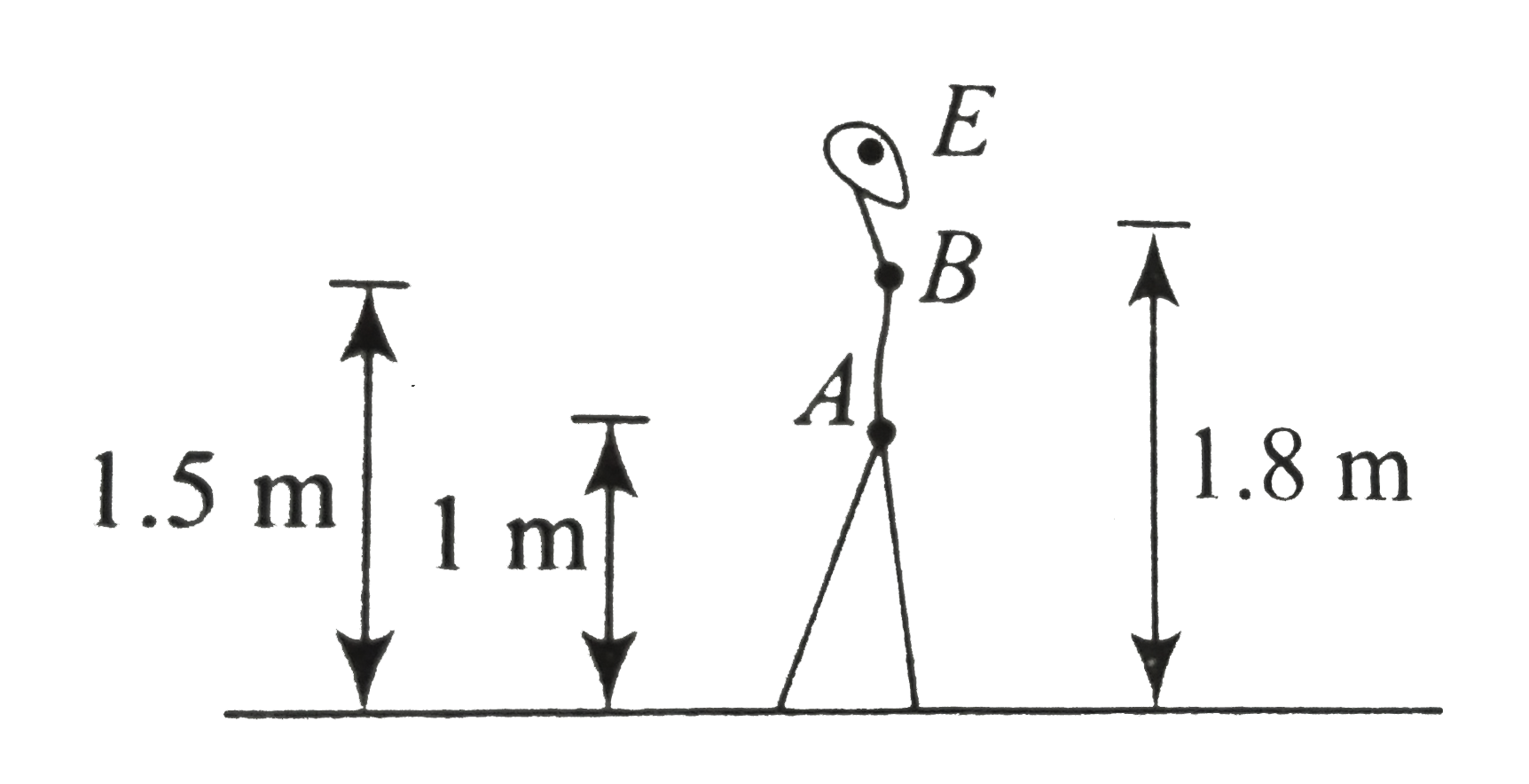
View SolutionA man is standing at distance x from a plane mirror in front of him. He wants to see the entire wall in mirror which is at distance. y behind the man. Find the minimum size of the mirror required.
View Solution
