Monochromatic light is refracted from air into the glass of refractive index μ . The ratio of the wavelength of incident and refracted waves is
(a)1:μ
(b)1:μ2
(c)μ:1
(d)1:1
The correct Answer is:3
To find the ratio of the wavelength of incident and refracted waves when monochromatic light is refracted from air into glass, we can follow these steps:
Step 1: Understand the refractive index
The refractive index (μ) of a medium is defined as the ratio of the speed of light in a vacuum (or air, approximately) to the speed of light in that medium. For air, we can consider the refractive index to be approximately 1. Therefore, we have:
- Refractive index of air (n_air) = 1
- Refractive index of glass (n_glass) = μ
Step 2: Apply Snell's Law
According to Snell's Law, the relationship between the angles of incidence (i) and refraction (r) is given by:
sin(i)sin(r)=nairnglass=1μ
Step 3: Relate speed and wavelength
The speed of light in a medium is related to its wavelength. The speed of light in air (v1) and in glass (v2) can be expressed in terms of their respective wavelengths (λ1 for air and λ2 for glass):
v1=f⋅λ1
v2=f⋅λ2
where f is the frequency of the light, which remains constant when light travels from one medium to another.
Step 4: Use the relationship between speed and refractive index
The refractive index can also be expressed in terms of the speeds of light in the two media:
μ=v1v2
Substituting the expressions for v1 and v2, we get:
μ=f⋅λ1f⋅λ2=λ1λ2
Step 5: Find the ratio of wavelengths
From the above equation, we can rearrange it to find the ratio of the wavelengths:
λ1λ2=μ
This means that the ratio of the wavelength of the incident light (in air) to the wavelength of the refracted light (in glass) is equal to the refractive index of the glass.
Final Result
Thus, the ratio of the wavelength of the incident wave to the refracted wave is:
λ1λ2=μ:1
Conclusion
The correct answer is that the ratio of the wavelength of incident and refracted waves is μ : 1.
---
The refractive index (μ) of a medium is defined as the ratio of the speed of light in a vacuum (or air, approximately) to the speed of light in that medium. For air, we can consider the refractive index to be approximately 1. Therefore, we have:
- Refractive index of air (n_air) = 1
- Refractive index of glass (n_glass) = μ
According to Snell's Law, the relationship between the angles of incidence (i) and refraction (r) is given by:
sin(i)sin(r)=nairnglass=1μ
The speed of light in a medium is related to its wavelength. The speed of light in air (v1) and in glass (v2) can be expressed in terms of their respective wavelengths (λ1 for air and λ2 for glass):
v1=f⋅λ1
v2=f⋅λ2
where f is the frequency of the light, which remains constant when light travels from one medium to another.
The refractive index can also be expressed in terms of the speeds of light in the two media:
μ=v1v2
Substituting the expressions for v1 and v2, we get:
μ=f⋅λ1f⋅λ2=λ1λ2
From the above equation, we can rearrange it to find the ratio of the wavelengths:
λ1λ2=μ
This means that the ratio of the wavelength of the incident light (in air) to the wavelength of the refracted light (in glass) is equal to the refractive index of the glass.
Thus, the ratio of the wavelength of the incident wave to the refracted wave is:
λ1λ2=μ:1
The correct answer is that the ratio of the wavelength of incident and refracted waves is μ : 1.
Topper's Solved these Questions
- RAY OPTICS Book:VMC MODULES ENGLISHChapter:RAY OPTICS Exercise:PRACTICE EXERCISE-8
Explore 6 Videos
- RAY OPTICS Book:VMC MODULES ENGLISHChapter:RAY OPTICS Exercise:PRACTICE EXERCISE-9
Explore 7 Videos
- RAY OPTICS Book:VMC MODULES ENGLISHChapter:RAY OPTICS Exercise:PRACTICE EXERCISE-7
Explore 6 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
- RAY OPTICS AND WAVE OPTICS Book:VMC MODULES ENGLISHChapter:RAY OPTICS AND WAVE OPTICS Exercise:IMPECCABLE
Explore 58 Videos
Similar Questions
A beam of monochromatic light is refracted from vacuum into a medium of refractive index 1.5 The wavelength of refracted light will be
View SolutionA beam o monochromatic light of wavelength λ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
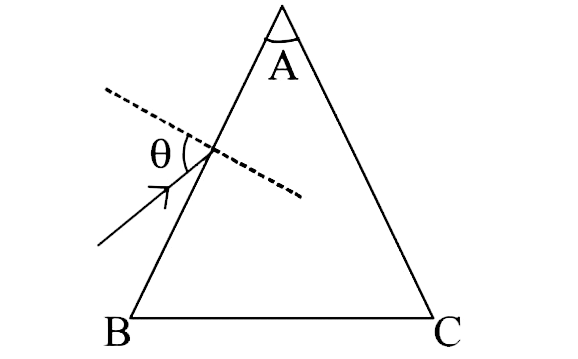
View SolutionMonochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
View SolutionA ray EF of monochromatic light is incident on the refracting surface AB of a regular glass prism ( refractive index=1.5) at angle of incidence i=55∘ (Figure). If it emerges the adjacent face AC, calculate the angle of emergence .e..
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA monochromatic beam of light of wavelength λ and frequency v goes from vacum to a medium of refractive index n. How do the wavelength and frequency of light change ?
View SolutionLight of wavelength 4500Å in vacuum enters into a glass block of refractive index 1.5. What is the wavelength of light in the glass block?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View Solution