The energy of a photon of wavelength λ is
hcλ
hcλ
λhc
λhc
The correct Answer is:B
To find the energy of a photon with a wavelength λ, we can follow these steps:
Step 1: Understand the relationship between energy and frequency
The energy E of a photon is directly proportional to its frequency ν. This relationship is given by the equation:
E=hν
where h is Planck's constant.
Step 2: Relate frequency to wavelength
We know the relationship between the speed of light c, frequency ν, and wavelength λ is given by:
c=νλ
From this equation, we can express frequency ν in terms of wavelength λ:
ν=cλ
Step 3: Substitute frequency into the energy equation
Now, we can substitute the expression for frequency ν into the energy equation:
E=hν=h(cλ)
Step 4: Simplify the equation
This simplifies to:
E=hcλ
This equation gives us the energy of a photon in terms of its wavelength λ.
Final Answer
Thus, the energy of a photon of wavelength λ is:
E=hcλ
---
The energy E of a photon is directly proportional to its frequency ν. This relationship is given by the equation:
E=hν
where h is Planck's constant.
We know the relationship between the speed of light c, frequency ν, and wavelength λ is given by:
c=νλ
From this equation, we can express frequency ν in terms of wavelength λ:
ν=cλ
Now, we can substitute the expression for frequency ν into the energy equation:
E=hν=h(cλ)
This simplifies to:
E=hcλ
This equation gives us the energy of a photon in terms of its wavelength λ.
Thus, the energy of a photon of wavelength λ is:
E=hcλ
Similar Questions
Momentum of a photon of wavelength λ is :
View SolutionThe ratio of the energy of a photon of 200Å wavelength radiation to that of 400Å radiation is :
View SolutionThe mass of photon of wavelength λ is given by
View SolutionThe ratio of the energy of a photon of 2000Å wavelength radiation to that of 4000Å radiation is
View SolutionThe follwing diagram indicates the energy levels of a certain atom when the system moves from 2E level to E, a photon of wavelength λ is emitted. The wavelength of photon produced during its transition from 4E3 level to E is

View SolutionA dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View SolutionCalculate the ratio of the energy of a photon of wavelength 3000 Å to that of a photon of wavelength 6000Å respectively
View SolutionCalculate the energy of a photon of blue light, λ=450 nm in air (or vacuum).
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be
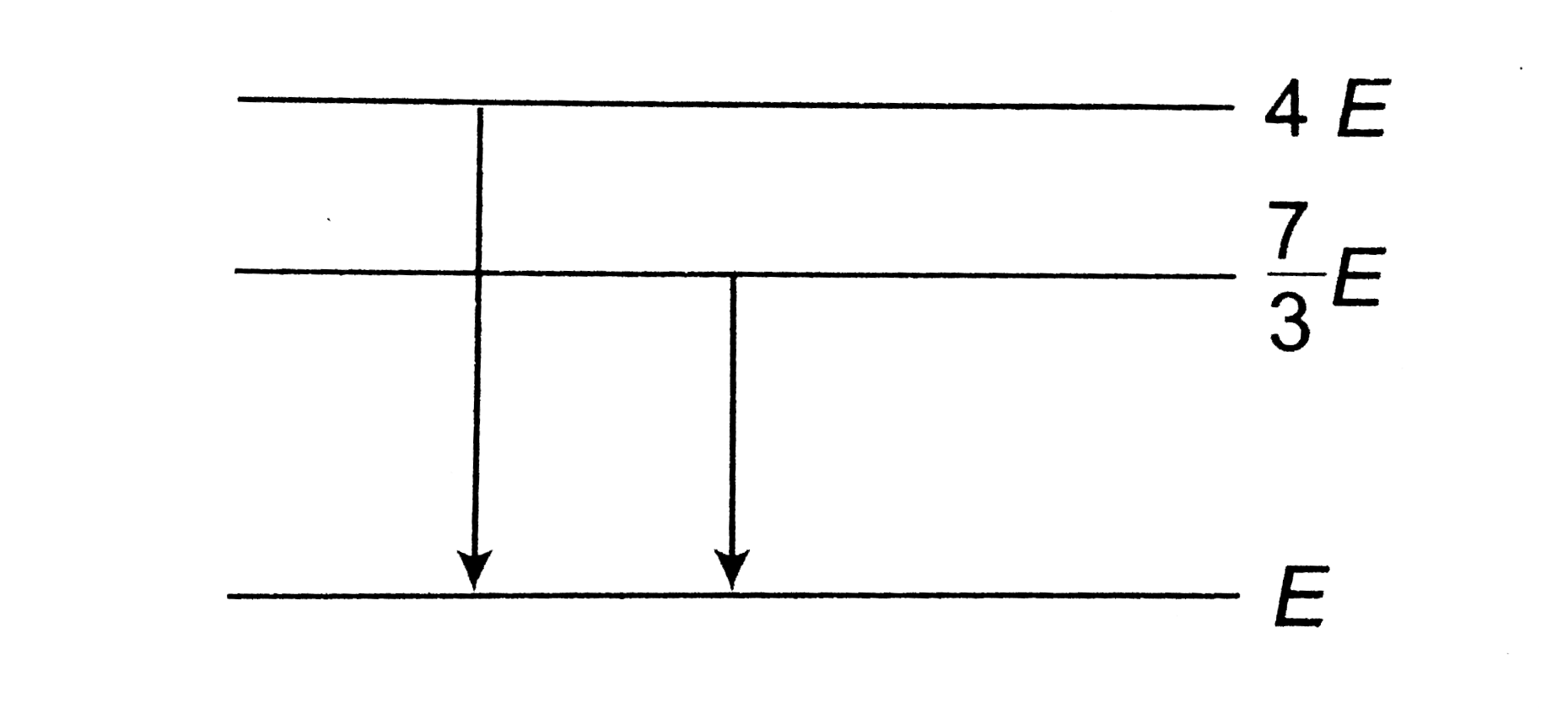
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be

View Solution