The mass of photon of wavelength λ is given by
hλc
h/λc
hc/λ
hλ/c
The correct Answer is:B
To find the mass of a photon in terms of its wavelength λ, we can follow these steps:
1. Understand the relationship between wavelength and momentum:
The de Broglie wavelength λ is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the photon.
2. Express momentum in terms of mass and velocity:
For a photon, the momentum p can also be expressed as:
p=mv
where m is the mass and v is the velocity. Since a photon travels at the speed of light c, we can write:
p=mc
3. Substitute the expression for momentum into the wavelength formula:
By substituting p=mc into the de Broglie wavelength equation, we have:
λ=hmc
4. Rearranging the equation to solve for mass:
To find the mass m of the photon, we can rearrange the equation:
mc=hλ
Dividing both sides by c gives:
m=hλc
5. Final expression for the mass of the photon:
Thus, the mass of the photon in terms of its wavelength λ is:
m=hλc
Conclusion:
The mass of a photon of wavelength λ is given by:
m=hλc
The de Broglie wavelength λ is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the photon.
For a photon, the momentum p can also be expressed as:
p=mv
where m is the mass and v is the velocity. Since a photon travels at the speed of light c, we can write:
p=mc
By substituting p=mc into the de Broglie wavelength equation, we have:
λ=hmc
To find the mass m of the photon, we can rearrange the equation:
mc=hλ
Dividing both sides by c gives:
m=hλc
Thus, the mass of the photon in terms of its wavelength λ is:
m=hλc
The mass of a photon of wavelength λ is given by:
m=hλc
Similar Questions
The energy of a photon of wavelength λ is
View SolutionMomentum of a photon of wavelength λ is :
View SolutionThe mass of photon having wavelength 1nm is :
View SolutionAn excited hydrogen atom emits a photon of wavelength λ in returning to the ground state. If 'R' is the Rydberg's constant, then the quantum number 'n' of the excited state is:
View SolutionAn excited hydrogen atom emits a photon of wavelength λ in returning to the ground state. If 'R' is the Rydberg's constant, then the quantum number 'n' of the excited state is:
View SolutionThe follwing diagram indicates the energy levels of a certain atom when the system moves from 2E level to E, a photon of wavelength λ is emitted. The wavelength of photon produced during its transition from 4E3 level to E is

View SolutionIf a hydrogen atom at rest, emits a photon of wavelength λ, the recoil speed of the atom of mass m is given by :
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be
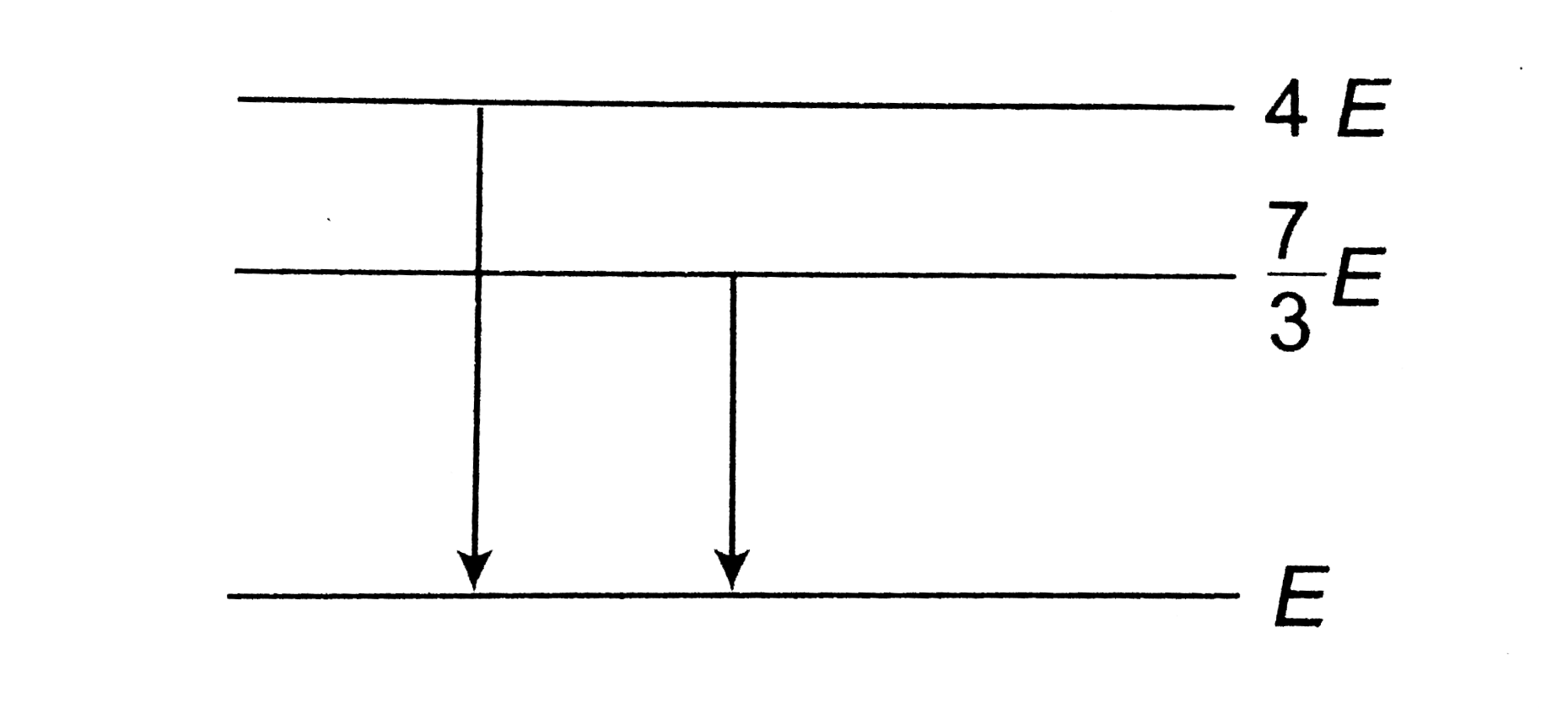
View SolutionThe following diagram indicates the energy levels of a certain atom when the system moves from 4E level to E. A photon of wavelength λ1 is emitted. The wavelength of photon produced during its transition from 73E level to E is λ2. the ratio λ1λ2 will be

View SolutionIf an electron in a hydrogen atom jumps from the 3rd orbit to the 2nd orbit, it emits a photon of wavelength λ. When it jumps form the 4th orbit to the 3dr orbit, the corresponding wavelength of the photon will be
View Solution
