A transistor -oscillator using a resonant circuit with an inductor L (of negligible resistance) and a capacitor C in series produce oscillations of frequency f. If L is doubled and C is changed to 4C, the frequency will be
f4
8f
f2√2
f2
The correct Answer is:C
To solve the problem, we need to analyze how the frequency of oscillation changes when the values of the inductor L and the capacitor C are modified.
1. Understand the formula for frequency in an LC circuit:
The frequency f of oscillation in a resonant LC circuit is given by the formula:
f=12π√LC
2. Identify the initial parameters:
Let the initial values of the inductor and capacitor be:
- Inductor: L
- Capacitor: C
Thus, the initial frequency f can be expressed as:
f=12π√LC
3. Modify the parameters as per the problem statement:
According to the question:
- The inductor is doubled: L′=2L
- The capacitor is changed to four times its original value: C′=4C
4. Substitute the new values into the frequency formula:
The new frequency f′ with the modified values is:
f′=12π√L′C′=12π√(2L)(4C)
5. Simplify the expression:
Now simplify the expression for f′:
f′=12π√8LC=12√2⋅2π√LC=12√2⋅12π√LC
Since 12π√LC=f, we can write:
f′=f2√2
6. Conclusion:
Therefore, the new frequency f′ after modifying the inductor and capacitor is:
f′=f2√2
Final Answer:
The frequency will be f2√2.
The frequency f of oscillation in a resonant LC circuit is given by the formula:
f=12π√LC
Let the initial values of the inductor and capacitor be:
- Inductor: L
- Capacitor: C
Thus, the initial frequency f can be expressed as:
f=12π√LC
According to the question:
- The inductor is doubled: L′=2L
- The capacitor is changed to four times its original value: C′=4C
The new frequency f′ with the modified values is:
f′=12π√L′C′=12π√(2L)(4C)
Now simplify the expression for f′:
f′=12π√8LC=12√2⋅2π√LC=12√2⋅12π√LC
Since 12π√LC=f, we can write:
f′=f2√2
Therefore, the new frequency f′ after modifying the inductor and capacitor is:
f′=f2√2
The frequency will be f2√2.
Similar Questions
In L − C oscillations
View SolutionPower factor in a series R-L-C resonant circuit is
View SolutionA resistor R, an inductor L and a capacitor C are connected in series to an oscillator of frequency n. If the resonant frequency is nr, then the current lags behind voltage, when
View SolutionAn AC of frequency f is flowing in a circuit containing a resistance R and capacitance C in series. The impedance of the circuit is equal to
View SolutionA resistor R,an inductor L, and a capacitor C are connected in series to an oscillator of freqency υ.if the resonant frequency is υr, then the current lags behind voltage, when:
View SolutionAn oscillator circuit consists of an inductance of 0.5mH and a capacitor of 20μF. The resonant frequency of the circuit is nearly
View SolutionIn an L-C-R series, AC circuit at resonance
View SolutionA resonant AC circuit contains a capacitor of capacitance 10−6F and an inductor of 10−4H. The frequency of electrical oscillation will be
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
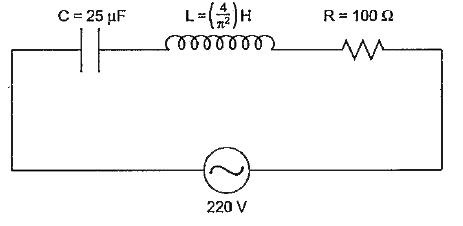
The resonant frequency of the given RLC circuit.
View SolutionAn L−C circuit consists of an inductor coil withh L=50.0mH and 20.0μF capacitor. There is negligible resistance in the circuit. The circuit is driven by a voltage source with V=V0cosωt. If V0=5.00mV and the frequency is twice the resonance frequency, determine.
a. the maximum charge on the capacitor.
b. the maximum current in the circuit.
c. the phase relationship between the voltages across the inductor, the capacitor and the sourse.
View Solution
