A resistor R,an inductor L, and a capacitor C are connected in series to an oscillator of freqency υ.if the resonant frequency is υr, then the current lags behind voltage, when:
v=0
v<vr
v=vr
v<ur
The correct Answer is:D
To solve the problem, we need to determine the condition under which the current lags behind the voltage in a series RLC circuit.
1. Understand the Circuit Behavior:
In a series RLC circuit, the voltage across the inductor (L) and capacitor (C) can cause the current to either lead or lag behind the voltage supplied by the oscillator.
2. Identify Reactances:
- The reactance of the inductor (X_L) is given by XL=ωL, where ω=2πν (with ν being the frequency).
- The reactance of the capacitor (X_C) is given by XC=1ωC.
3. Condition for Current Lagging:
The current lags behind the voltage when the reactance of the inductor is greater than the reactance of the capacitor:
XL>XC
Substituting the expressions for reactance:
ωL>1ωC
4. Manipulate the Inequality:
Multiplying both sides by ωC (assuming ω and C are positive):
ω2LC>1
5. Rearranging the Terms:
This can be rearranged to:
ω2>1LC
6. Taking the Square Root:
Taking the square root of both sides gives:
ω>1√LC
7. Substituting for Frequency:
Since ω=2πν, we can substitute this into the inequality:
2πν>1√LC
8. Final Condition:
Dividing both sides by 2π:
ν>12π√LC
9. Relating to Resonant Frequency:
The resonant frequency νr of the circuit is given by:
νr=12π√LC
Therefore, we can conclude:
ν>νr
Conclusion:
The current lags behind the voltage when the frequency ν is greater than the resonant frequency νr.
In a series RLC circuit, the voltage across the inductor (L) and capacitor (C) can cause the current to either lead or lag behind the voltage supplied by the oscillator.
- The reactance of the inductor (X_L) is given by XL=ωL, where ω=2πν (with ν being the frequency).
- The reactance of the capacitor (X_C) is given by XC=1ωC.
The current lags behind the voltage when the reactance of the inductor is greater than the reactance of the capacitor:
XL>XC
Substituting the expressions for reactance:
ωL>1ωC
Multiplying both sides by ωC (assuming ω and C are positive):
ω2LC>1
This can be rearranged to:
ω2>1LC
Taking the square root of both sides gives:
ω>1√LC
Since ω=2πν, we can substitute this into the inequality:
2πν>1√LC
Dividing both sides by 2π:
ν>12π√LC
The resonant frequency νr of the circuit is given by:
νr=12π√LC
Therefore, we can conclude:
ν>νr
The current lags behind the voltage when the frequency ν is greater than the resonant frequency νr.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SECTION E:
6 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - PART II:
6 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SECTION C
16 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
Similar Questions
A resistor R, an inductor L and a capacitor C are connected in series to an oscillator of frequency n. If the resonant frequency is nr, then the current lags behind voltage, when
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
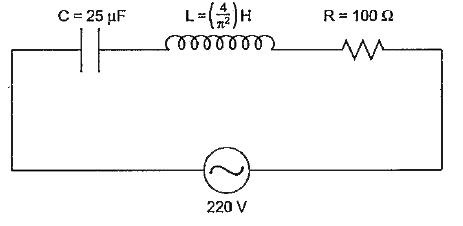
The resonant frequency of the given RLC circuit.
View SolutionThe frequency of oscillation of current in the indcutor is

View SolutionA resistor R an inductance L and a capacitor C are all connected in series with an ac supply The resistance of R is 16ohm and for the given frequency the inductive reactance of L is 24 ohm and the capacitive reactance of C is 12ohm If the current in the circuit is 5A find
(a) the potential difference across R,L and C
(b) the impedance of the circuit
(c) the voltage of the ac supply and
(d) the phase angle .
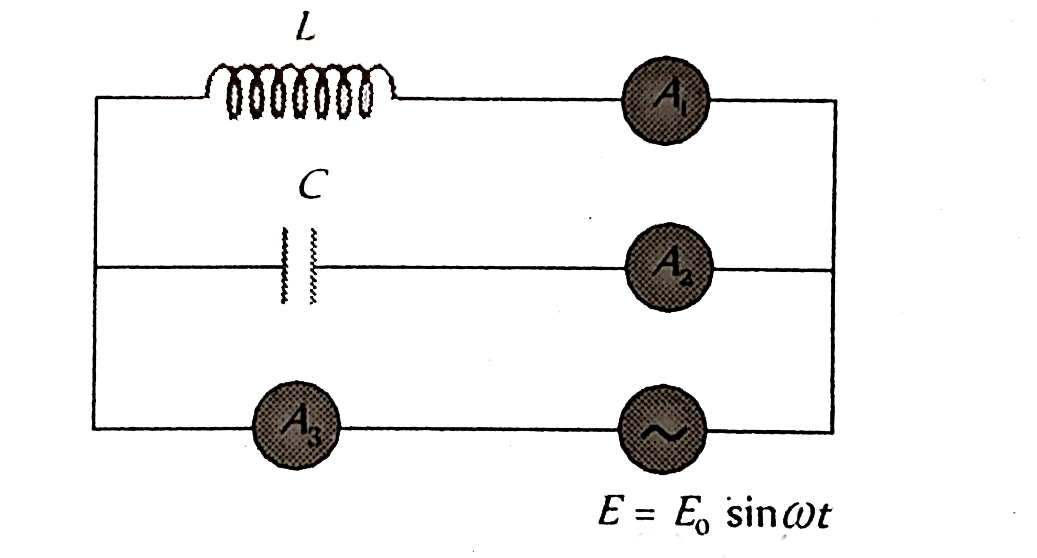
View SolutionAn inductor L and a capacitor C are connected in the circuit as shown in the figure. The frequency of the power supply is equal to the resonant frequency of the circuit. Which ammeter will read zero ampere
View SolutionIf a 0.03 H inductor, a 10Ω resistor and a 2μF capacitor are connected in series. At what frequency will they resonate? What will be the phase angle at resonance?
View SolutionAt resonance in series R-L-C circuit
_PHY_E06_308_Q01.png)
View SolutionA capacitor, a resistor and a 40 mH inductor are connected in series to an a.c. source of frequency 60 Hz. Calculate the capacitance of the capacitor,if current is in phase with the voltage.
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
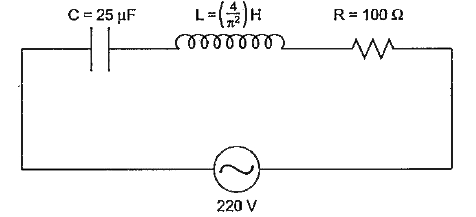
Current flowing through the circuit.
View SolutionAn inductor L and a resistor R are connected in series to a battery, through a key/switch. Show graphically, how current decreases with time when the key/switch is opened.
View Solution
