The unit of Stefan's constant σ is
W−m2−K4
W−m2/K4
W/m2−K
W/m2−K4
The correct Answer is:d
To determine the unit of Stefan's constant (σ), we start from the equation that relates power (P) to σ:
1. Understanding the Equation: The power radiated by a black body is given by the equation:
P=σ⋅A⋅T4
where:
- P = Power (in Watts)
- σ = Stefan's constant
- A = Area (in square meters, m2)
- T = Temperature (in Kelvin, K)
2. Rearranging the Equation: To find the unit of σ, we can rearrange the equation:
σ=PA⋅T4
3. Substituting the Units: Now we substitute the units for each quantity:
- Power (P) has the unit of Watts (W).
- Area (A) has the unit of square meters (m2).
- Temperature (T) has the unit of Kelvin (K).
Therefore, we can express the units as follows:
σ=Wm2⋅K4
4. Expressing Watts in Base Units: We know that 1 Watt (W) is equivalent to 1J/s (Joules per second). Joules can be expressed in base units as 1J=1kg⋅m2/s2. Thus:
W=kg⋅m2s3
5. Substituting Back: Now substituting this back into our equation for σ:
σ=kg⋅m2/s3m2⋅K4
6. Simplifying the Units: The m2 in the numerator and denominator cancels out:
σ=kgs3⋅K4
7. Final Unit of Stefan's Constant: Therefore, the unit of Stefan's constant σ is:
σ=kgs3⋅K4
Summary:
The unit of Stefan's constant σ is kgs3⋅K4.
P=σ⋅A⋅T4
where:
- P = Power (in Watts)
- σ = Stefan's constant
- A = Area (in square meters, m2)
- T = Temperature (in Kelvin, K)
σ=PA⋅T4
- Power (P) has the unit of Watts (W).
- Area (A) has the unit of square meters (m2).
- Temperature (T) has the unit of Kelvin (K).
σ=Wm2⋅K4
W=kg⋅m2s3
σ=kg⋅m2/s3m2⋅K4
σ=kgs3⋅K4
σ=kgs3⋅K4
The unit of Stefan's constant σ is kgs3⋅K4.
Similar Questions
Unit of Stefan's constant is
View SolutionWhat is Stefan's constant ?
View SolutionThe units of cell constant are
View SolutionCalculate the temperature at which a perfect black body radiates at the rate of 1Wcm−2 , value of Stefan's constant,
σ=5.67×10−5Wm−2K−8
View SolutionAssume that the total surface area of a human body is 1.6m2 and that it radiates like an ideal radiator. Calculate the amount of energy radiates per second by the body if the body temperature is 37∘C . Stefan constant σ is 6.0×10−8Wm−2K−4 .
View SolutionOne end of a rod of length 20cm is inserted in a furnace at 800K The sides of the rod are covered with an insulating material and the other end emits radiation like a black body. The temperature of this end is 750K in the steady state The temperature of the surrounding air is 300K Assuming radiation to be the only important mode of energy transfer between the surrounding and the open end of the rod, find the thermal conductivity of the rod Stefan's constant σ=6.0×10−8Wm−2K−4 .
View SolutionA metallic sphere having radius 0.08m and mass m=10kg is heated to a temperature of 227∘C and suspended inside a box whose walls ae at a temperature of 27∘C. The maximum rate at which its temperature will fall is:-
(Take e=1, Stefan's constant σ=5.8×10−8W/m−2K−4 and specific heat of the metal s=90cal/kg/degJ=4.2Joules/Calorie)
View SolutionThe operating temperature of a tungesten filament in an indandescent lamp is 2000K and its emissivity is 0.3.
Find the surface area of the filament of a 25 watt lamp. Stefan's constant σ=5.67×10−8Wm−2K−4
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
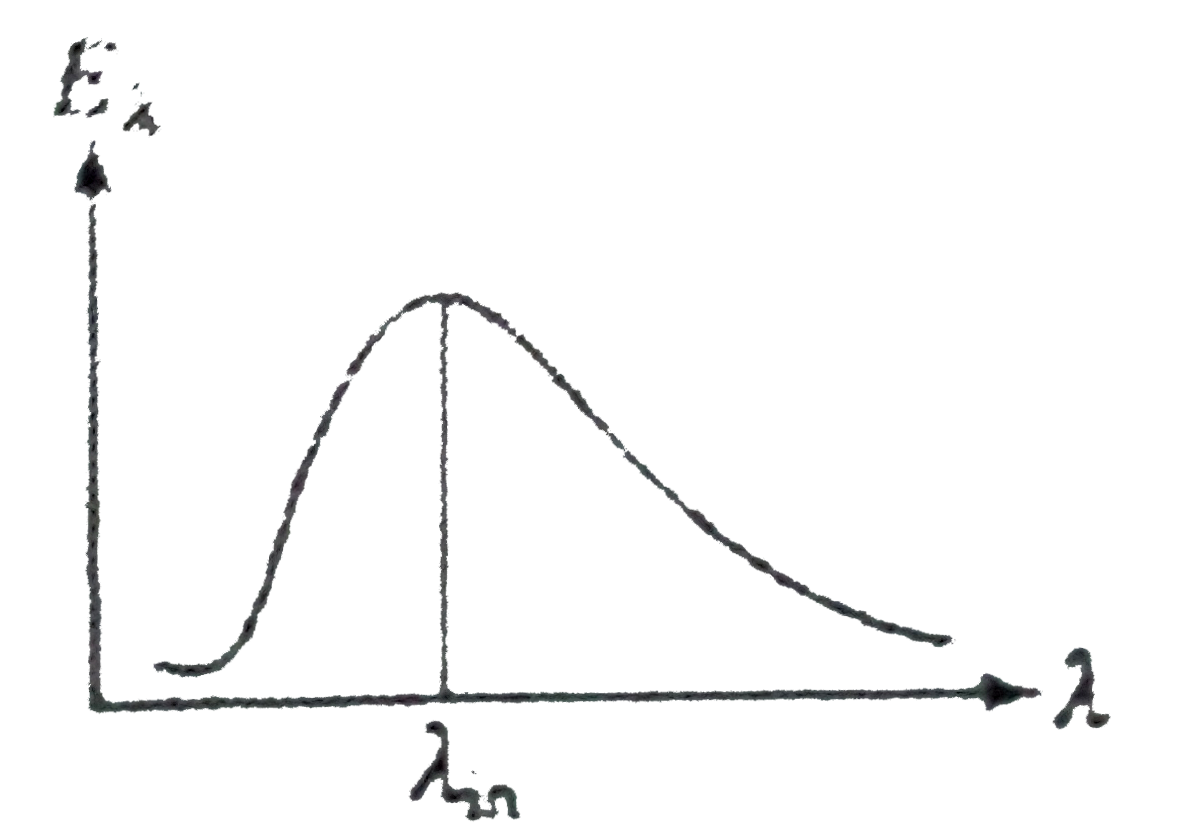
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionThe radiations emitted by the sun are analyzed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
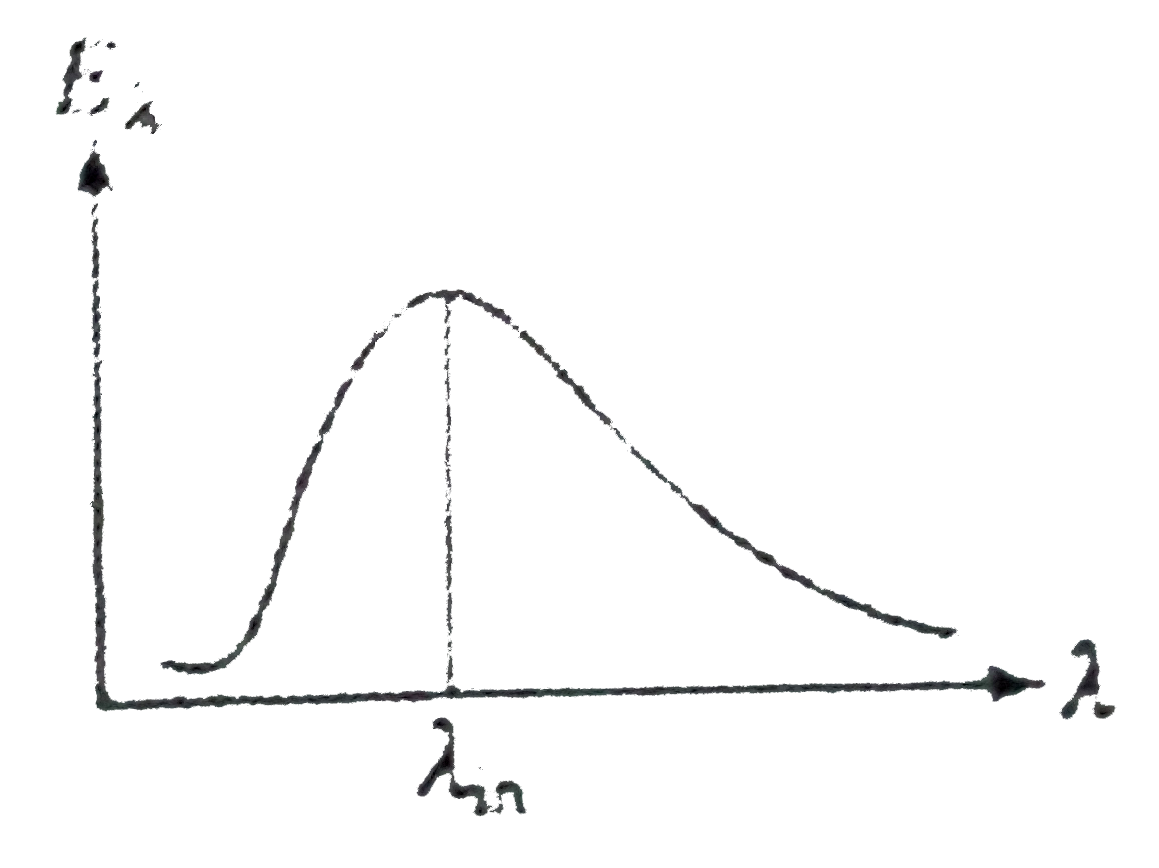
Assume the sun produces energy only by nuclear fusion of hydrogen nuclei and the fraction of nuclear mass of hydrogen that can be converted to energy is η. How long will the sun keep on emittied the energy if the mass of hydrogen at present in Sun's core is m?
View Solution
