The operating temperature of a tungesten filament in an indandescent lamp is 2000K and its emissivity is 0.3.
Find the surface area of the filament of a 25 watt lamp. Stefan's constant σ=5.67×10−8Wm−2K−4
To find the surface area of the tungsten filament in a 25-watt incandescent lamp, we can use Stefan-Boltzmann's law, which relates the power radiated by a black body to its temperature and surface area. The formula is given by:
W=A⋅ε⋅σ⋅T4
Where:
- W is the power (in watts),
- A is the surface area (in square meters),
- ε is the emissivity (dimensionless),
- σ is the Stefan-Boltzmann constant (5.67×10−8Wm−2K−4),
- T is the absolute temperature (in Kelvin).
1. Identify the given values:
- Power W=25W
- Emissivity ε=0.3
- Temperature T=2000K
- Stefan-Boltzmann constant σ=5.67×10−8Wm−2K−4
2. Rearrange the formula to solve for the surface area A:
A=Wε⋅σ⋅T4
3. Calculate T4:
T4=(2000K)4=(2×103)4=16×1012K4
4. Substitute the values into the area formula:
A=250.3⋅(5.67×10−8)⋅(16×1012)
5. Calculate the denominator:
- First, calculate 0.3⋅5.67×10−8:
0.3⋅5.67×10−8=1.701×10−8
- Then multiply by 16×1012:
1.701×10−8⋅16×1012=2.7136×105
6. Now calculate the surface area A:
A=252.7136×105≈0.000092m2
7. Convert to square meters:
A≈0.918m2
Final Answer:
The surface area of the tungsten filament is approximately 0.918m2.
- W is the power (in watts),
- A is the surface area (in square meters),
- ε is the emissivity (dimensionless),
- σ is the Stefan-Boltzmann constant (5.67×10−8Wm−2K−4),
- T is the absolute temperature (in Kelvin).
- Power W=25W
- Emissivity ε=0.3
- Temperature T=2000K
- Stefan-Boltzmann constant σ=5.67×10−8Wm−2K−4
A=Wε⋅σ⋅T4
T4=(2000K)4=(2×103)4=16×1012K4
A=250.3⋅(5.67×10−8)⋅(16×1012)
- First, calculate 0.3⋅5.67×10−8:
0.3⋅5.67×10−8=1.701×10−8
- Then multiply by 16×1012:
1.701×10−8⋅16×1012=2.7136×105
A=252.7136×105≈0.000092m2
A≈0.918m2
The surface area of the tungsten filament is approximately 0.918m2.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
83 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The operating temperature of an in candescent bulb (with tungsten filament) of power 60 W is 3000 K. If the surface area of the filament be 25 mm2, find its emissivity e.
View SolutionA solid metallic sphere of diameter 20 cm and mass 10 kg is heated to a temperature of 327∘C and suspended in a box in which a constant temperature of 27∘C is maintained. Find the rate at which the temperature of the Sphere will fall with time. Stefan's constant=5.67×10−8W/m2/K4 and specific heat of metal =420J/kg/∘C.
View SolutionCalculate the power of an incandescent lamp whose filament has a surface area of 0.19cm2 and is at a temperature of 3645K. Emmisivity of the surface is 0.4, σ=5.7×10−8Wm−2K−4 ?
View SolutionCalculate the temperature at which a perfect black body radiates at the rate of 1Wcm−2 , value of Stefan's constant,
σ=5.67×10−5Wm−2K−8
View SolutionA metallic sphere having radius 0.08m and mass m=10kg is heated to a temperature of 227∘C and suspended inside a box whose walls ae at a temperature of 27∘C. The maximum rate at which its temperature will fall is:-
(Take e=1, Stefan's constant σ=5.8×10−8W/m−2K−4 and specific heat of the metal s=90cal/kg/degJ=4.2Joules/Calorie)
View SolutionCalculate the energy radiated per minute from a filament of an incandescent lamp at 3,000 K if the surface area is 10−4m2 and its relative emitted is 0.425.
View SolutionCalculate the energy radiated per minute by a black body of surface area 200cm2 , maintained at 127∘C. σ=5.7×10−8Wm−2K−4
View SolutionA solid body X of very large heat capacity is kept in an atmosphere whose temperature is 300 K. The body X is connected to a rod of length 1 m and cross sectional area S, as shown in the figure. Thermal conductivity of rod AB is 0.0567W/mK. Assuming that there is no heat exchange with the surrounding except fom the end B of the rod i.e., neither by any surface of X nor by the curved surface of rod. The end B has emissivity e=0.8. If the steady state temperature of the end B is 400 K then find the temperature of X in steady state. (Stefan constant σ−5.67×10−8W/m2K4)
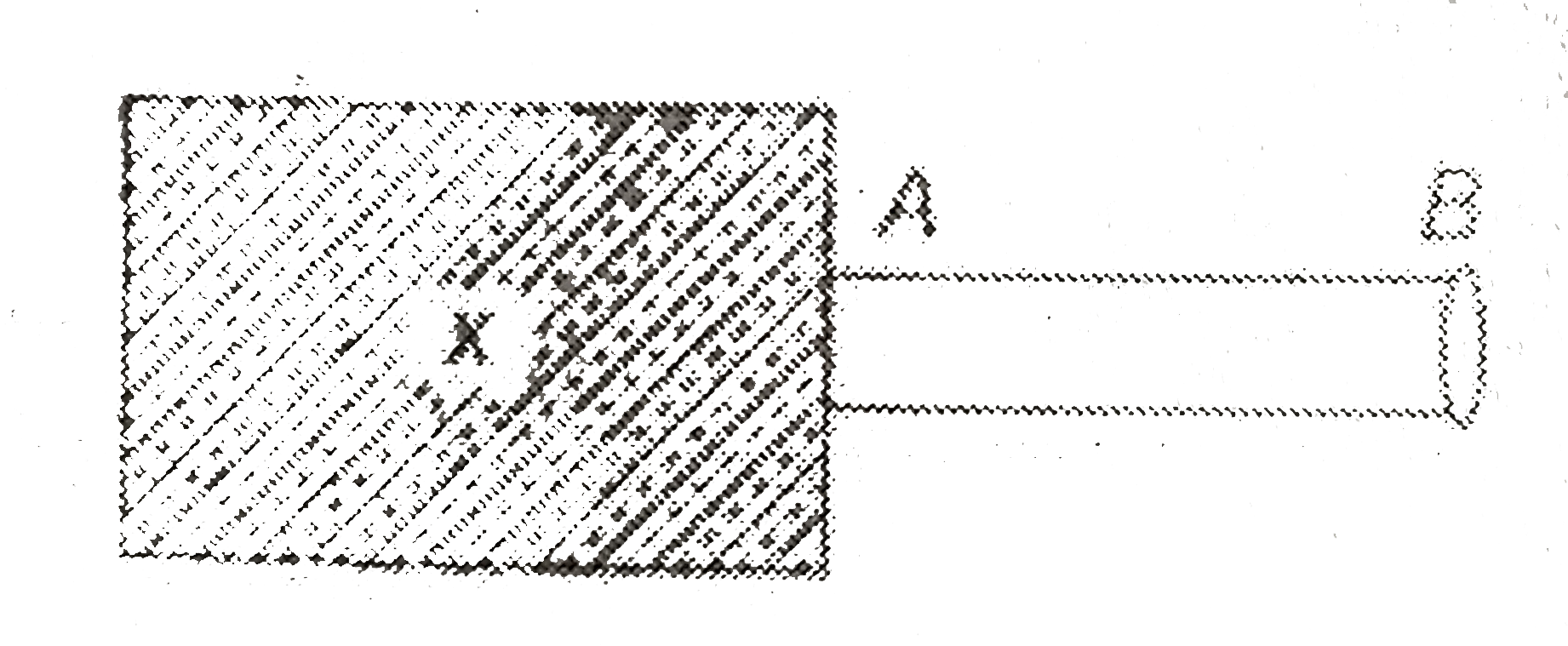
View SolutionIf the filament of a 100 W bulb has an area 0.25cm2 and behaves as a perfect black body. Find the wavelength corresponding to the maximum in its energy distribution. Given that Stefan's constant is σ=5.67×10−8J/m2sK4.
View SolutionIf the filament of a 100 W bulb has an area 0.25cm2 and behaves as a perfect block body. Find the wavelength corresponding to the maximum in its energy distribution. Given that Stefan's constant is σ=5.67×10−8J/m2sK4.
View Solution
