A solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
h = R
h = 2R
h = 0
No relation between h and R
The correct Answer is:D
To solve the problem of finding the maximum acceleration of the center of mass of a solid sphere when a horizontal force F is applied at a height h from the lowest point, we can follow these steps:
1. Identify the Forces Acting on the Sphere:
- The only external force acting on the sphere is the horizontal force F. Since the surface is smooth, there is no friction.
2. Determine the Acceleration of the Center of Mass:
- The acceleration of the center of mass acm can be calculated using Newton's second law. The net force acting on the sphere is F.
- The mass of the sphere is m.
- Therefore, the acceleration of the center of mass is given by:
acm=Fm
3. Analyze the Effect of Height h:
- The height h from which the force is applied does not affect the acceleration of the center of mass directly.
- The force F will cause the sphere to translate without rotation since there is no friction to create a torque about the center of mass.
4. Conclusion:
- The acceleration of the center of mass acm is independent of the height h from which the force is applied. Thus, for any height h, the maximum acceleration of the center of mass remains:
acm=Fm
Final Result:
The maximum acceleration of the center of mass of the sphere is given by:
acm=Fm
- The only external force acting on the sphere is the horizontal force F. Since the surface is smooth, there is no friction.
- The acceleration of the center of mass acm can be calculated using Newton's second law. The net force acting on the sphere is F.
- The mass of the sphere is m.
- Therefore, the acceleration of the center of mass is given by:
acm=Fm
- The height h from which the force is applied does not affect the acceleration of the center of mass directly.
- The force F will cause the sphere to translate without rotation since there is no friction to create a torque about the center of mass.
- The acceleration of the center of mass acm is independent of the height h from which the force is applied. Thus, for any height h, the maximum acceleration of the center of mass remains:
acm=Fm
The maximum acceleration of the center of mass of the sphere is given by:
acm=Fm
Similar Questions
A solid sphere of radius R is resting on a smooth horizontal surface. A constant force F is applied at a height h from the bottom. Choose the correct alternative.

View SolutionA uniform sphere is place on a smooth horizontal surface and as horizontal force F is appied on it at a distance h above the surface. The acceleratioin of the centre
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA solid sphere rests on a horizontal surface. A horizontal impulse is applied at height h from centre. The sphere starts rolling just after the application of impulse. The ratio h/R will be
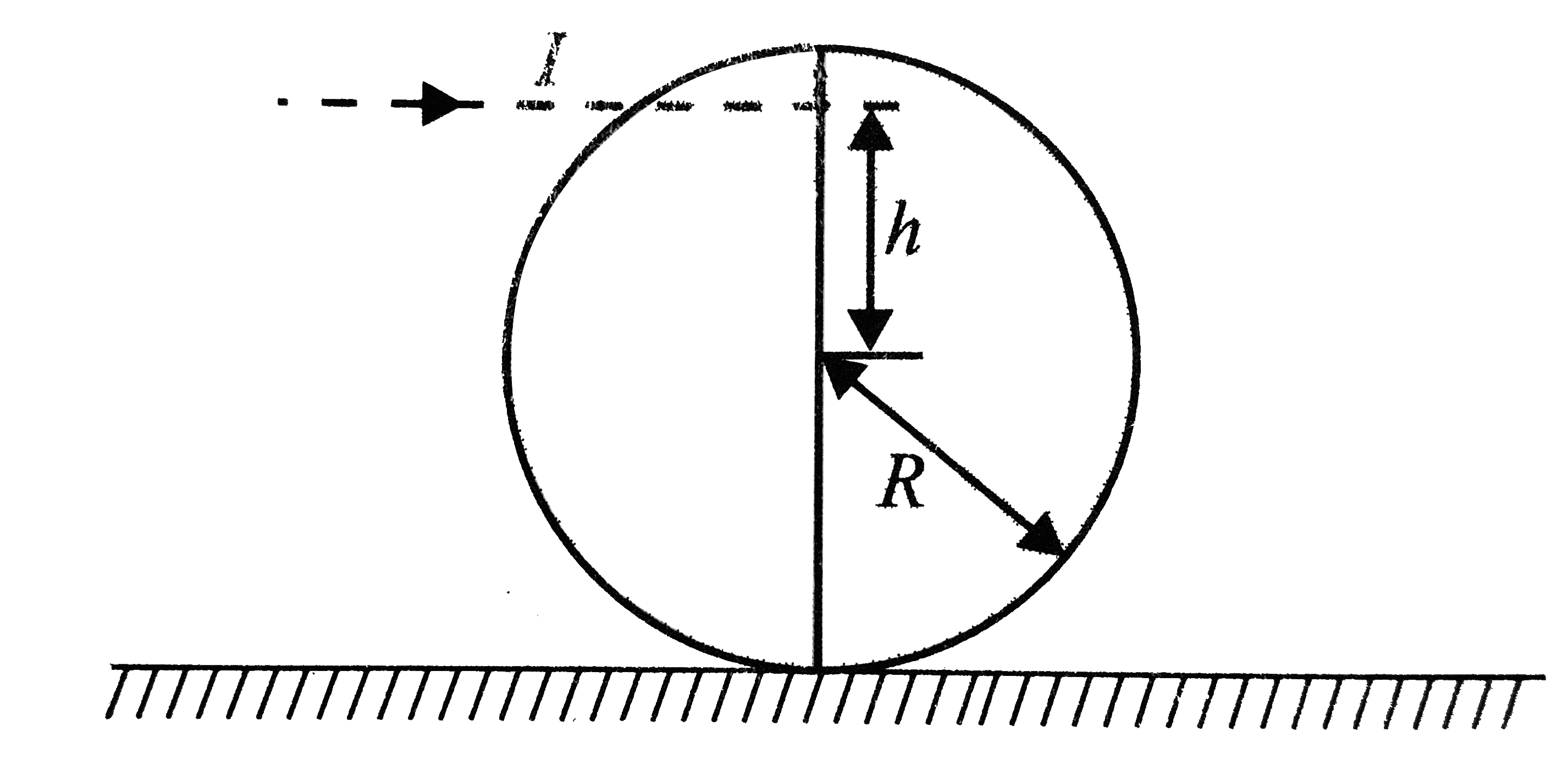
View SolutionA solid sphere of mass M and radius R is placed on a rough horizontal surface. It is stuck by a horizontal cue stick at a height h above the surface. The value of h so that the sphere performs pure rolling motion immediately after it has been stuck is

View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionA wire is wrapped N times over a solid sphere of mass m which is place on a smooth horizontal surface. A horizontal magnetic field of induction →B is present. Find the (a) torque (b) angular acceleration experienced by the sphere. Assume that the mass of the wire is negligible compared to the mass of the sphere.
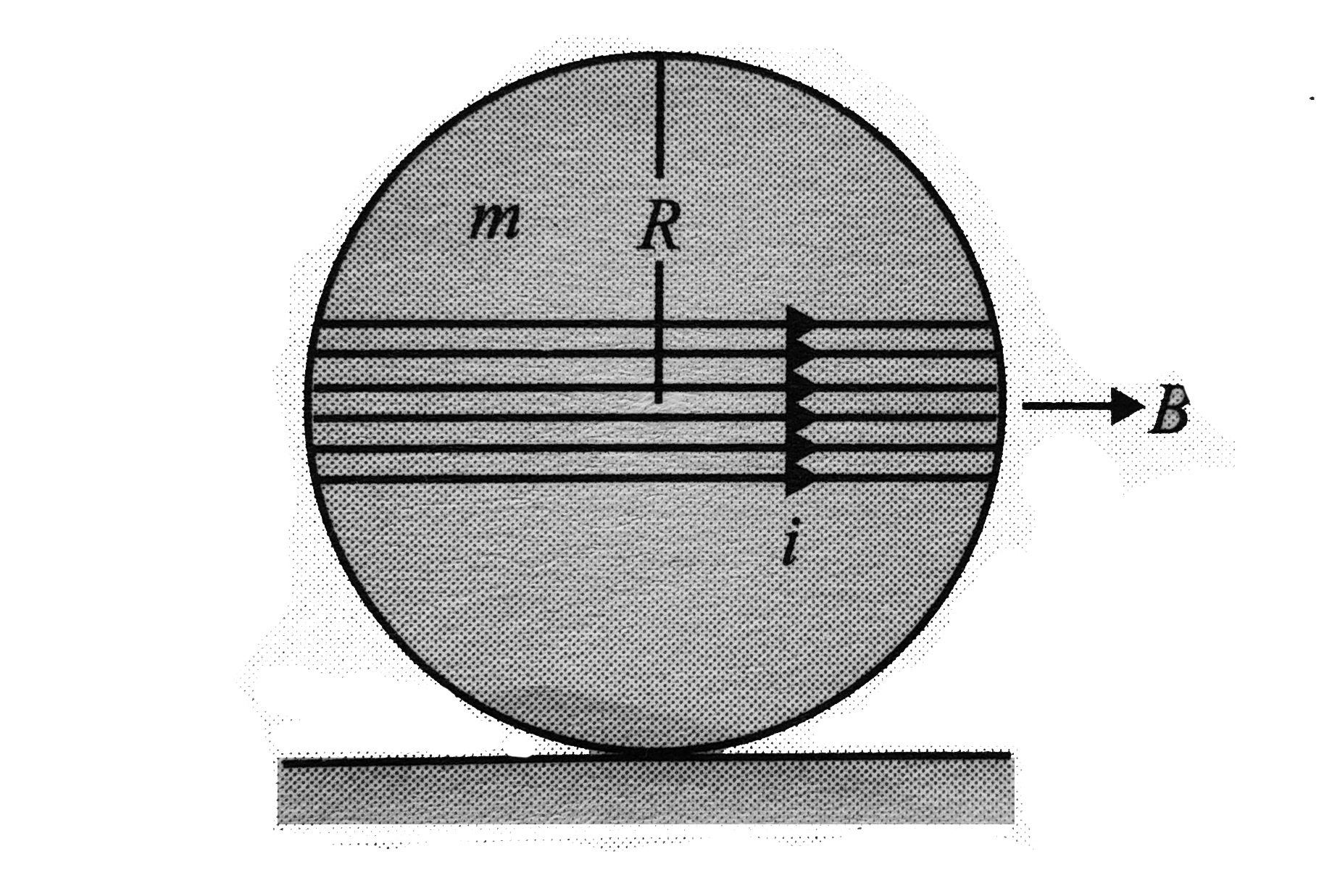
View Solution
