Two parallel metal plates having charges +Q and −Q face each other at a certain distance between them.If the plates are now dipped in kerosene oil tank ,the electric field between the plates will
increase
decrease
remain same
become zero
The correct Answer is:B
To solve the problem regarding the effect of dipping charged parallel plates into kerosene oil on the electric field between them, we can follow these steps:
1. Understand the Initial Setup:
- We have two parallel metal plates with charges +Q and -Q facing each other.
- The area of the plates is denoted as A.
- The surface charge density (σ) on the plates is given by:
σ=QA
2. Electric Field in Air:
- The electric field (E) between the plates in air (or vacuum) can be expressed using the formula:
E=σϵ0
- Substituting the expression for σ, we get:
E=QAϵ0
- Here, ε₀ is the permittivity of free space.
3. Introducing Kerosene Oil:
- When the plates are dipped in kerosene oil, the medium between the plates changes.
- The relative permittivity (dielectric constant) of kerosene oil is denoted as ε_r.
4. Electric Field in Kerosene Oil:
- The electric field between the plates when kerosene oil is present can be expressed as:
E′=σϵ0ϵr
- Substituting for σ, we have:
E′=QAϵ0ϵr
5. Comparing Electric Fields:
- Since ε_r (the dielectric constant of kerosene oil) is greater than 1, the electric field in kerosene oil (E') will be:
E′=QAϵ0ϵr<QAϵ0=E
- This indicates that the electric field decreases when the plates are submerged in kerosene oil.
6. Conclusion:
- Therefore, the electric field between the plates will decrease when they are dipped in kerosene oil.
Final Answer:
The electric field between the plates will decrease.
- We have two parallel metal plates with charges +Q and -Q facing each other.
- The area of the plates is denoted as A.
- The surface charge density (σ) on the plates is given by:
σ=QA
- The electric field (E) between the plates in air (or vacuum) can be expressed using the formula:
E=σϵ0
- Substituting the expression for σ, we get:
E=QAϵ0
- Here, ε₀ is the permittivity of free space.
- When the plates are dipped in kerosene oil, the medium between the plates changes.
- The relative permittivity (dielectric constant) of kerosene oil is denoted as ε_r.
- The electric field between the plates when kerosene oil is present can be expressed as:
E′=σϵ0ϵr
- Substituting for σ, we have:
E′=QAϵ0ϵr
- Since ε_r (the dielectric constant of kerosene oil) is greater than 1, the electric field in kerosene oil (E') will be:
E′=QAϵ0ϵr<QAϵ0=E
- This indicates that the electric field decreases when the plates are submerged in kerosene oil.
- Therefore, the electric field between the plates will decrease when they are dipped in kerosene oil.
The electric field between the plates will decrease.
Similar Questions
Two metal plates having charges Qand−Q face each other at some separation and are dipped into an oil tank .If the oil is pumped out, the eletric field between the plates will
View SolutionDerive an expression for the capacitance of a parallel plate capacitor in terms of the areas of the plates and the distance between them. Assume there is a vacuum in between the plates with the electric field between the plates E=σε0 (where the symbols have their usual meaning).
View Solution
Knowledge Check
As the distance between the plates of a parallel plate capacitor decreased
AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
Two plates are 2cm apart, a potential difference of 10 volt is applied between them, the electric field between the plates is
View SolutionConsider a parallel plate capacitor having charge Q. Then,
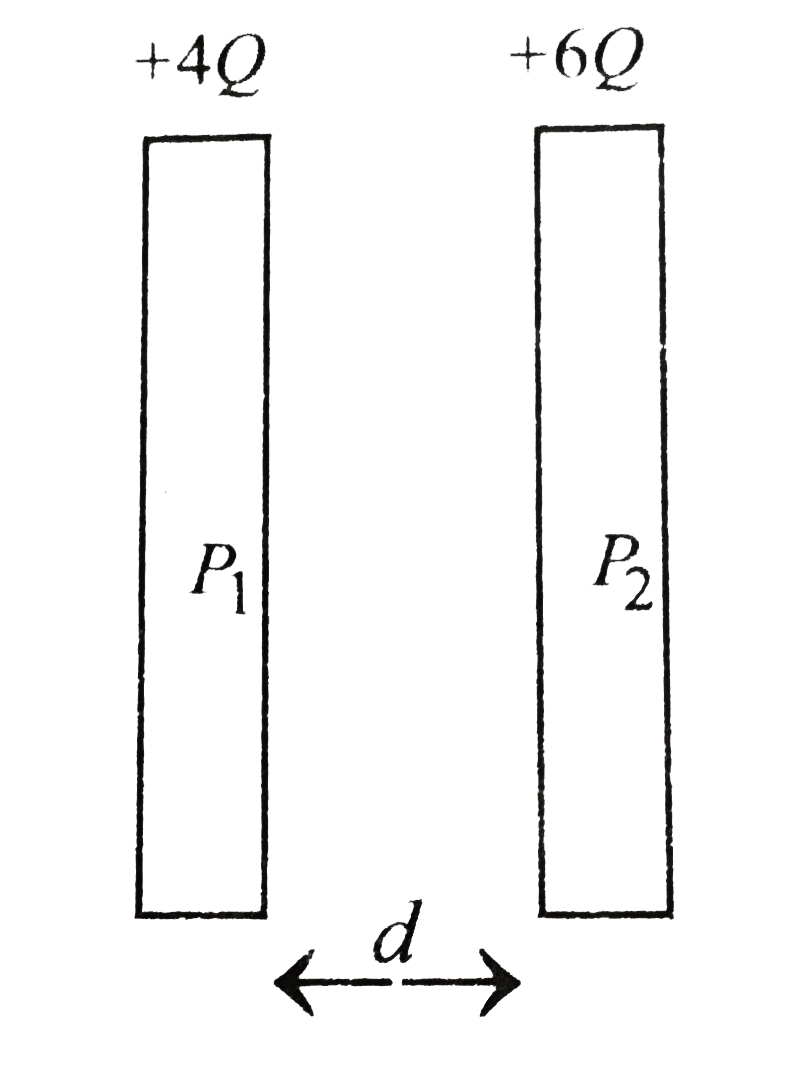
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
View SolutionTwo large conducting plates of a parallel plate capacitor are given charges Q and 3Q respectively. If the electric field in the region between the plates is E0 , then the force of interaction between the plates is

View SolutionEach of two large conducting parallel plates has one sided surface area A. If one of the plates is given a charge Q whereas the other is neutral, then the electric field at a point in between the plates is given by
View SolutionPositive charge q is given to each plate of a parallel plate air capacitor having area of each plate A and seperation between them, d. Then find
(i) Capacitance of the system. (ii) Charges appearing on each surface of plates
(iii) Electric field between the plates (iv) Potential diffrence between the plates
(v) Energy stored between hte plates
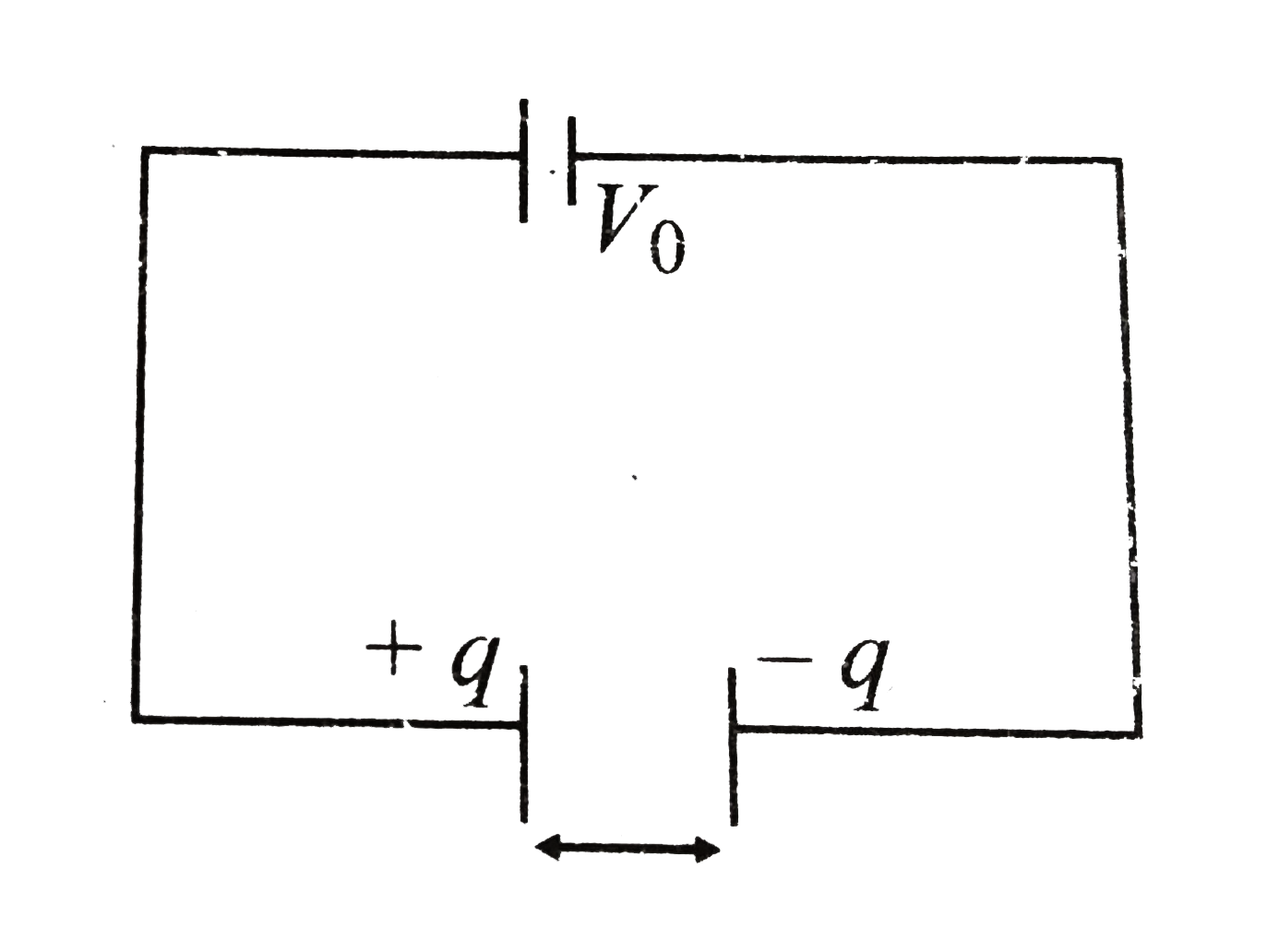
View SolutionTwo plates of a parallel plate capacitor carry charges q and -q and are separated by a distance a from each other. The capacitor is connected to a constant voltage source V0. The distance between the plates is changed to x+dx. Then in steady state.
View Solution
