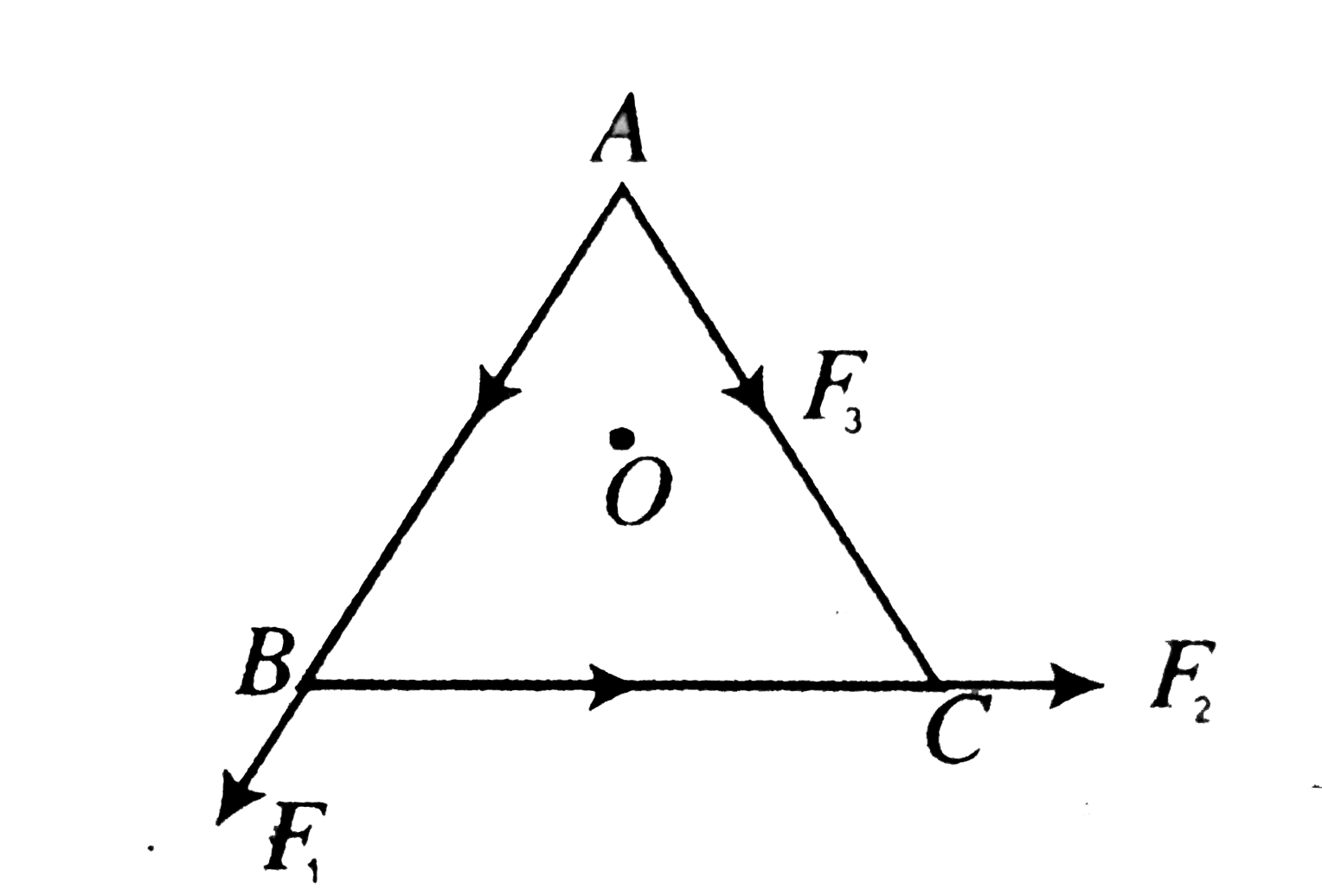
ABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is

a. F1+F22
b. 2(F1+F2)
c. F1+F2
d. F1−F2
The correct Answer is:C
Taking anticlockwise torque
F1d+F2d−F3d=0 (where d= perpendicular distance of the centre O from each side)
∴F3=F1+F2
Similar Questions
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC and G is the centroid of the triangle, then −−→GD+−−→GE+−−→GF=
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
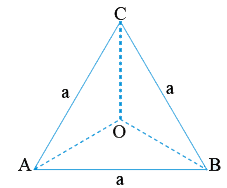
−−→AB+−−→BC+−−→CA
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
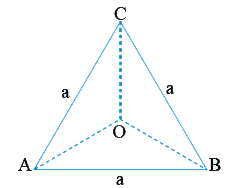
If −−→AB+−−→AC=n−−→AO then n = ?
View SolutionABC is an equilateral triangle. Length of each side is 'a' and centroid is point O. Find
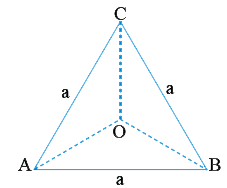
If ∣∣∣−−→AB+−−→BC+−−→AC∣∣∣=na then n = ?
View SolutionIf D, E, F are respectively the mid-points of AB, AC and BC respectively in a ΔABC, then −−→BE+−−→AF=
View SolutionThree forces →F1,→F2 and →F3 are represented as shown. Each of them is equal magnitude.
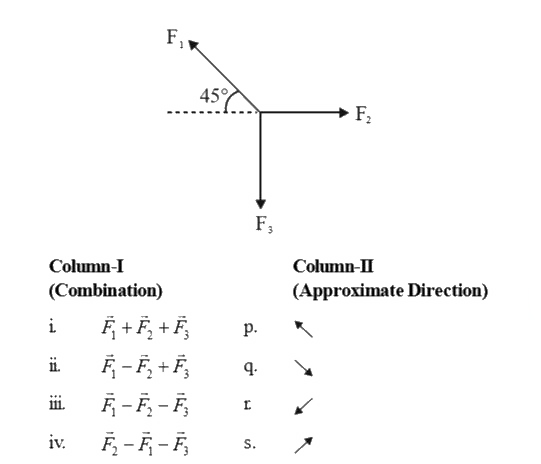
Now match the given columns and select the correct option from the codes given below.
View SolutionABC is isosceles triangle, right angled at A. The resultant of the forces acting along −−→AB,−−→AC with magnitudes 1AB and 1AC respectively is the force along −−→AD, where D is the foot of the perpendicular from A on BC. The magnitude of the resultant is:
View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
View Solution