The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment →p is given by (r >> seperation of two charges forming dipole , ε0 = permittivity of free space
→E=→P4πε0r3
→E=2→P4πε0r3
→E=−→P4πε0r2
→E=−→P4πε0r3
The correct Answer is:D
Step by step video & image solution for The electric field at a point on the equatorial plane at a distance r from the centre of a dipole having dipole moment vecp is given by (r >> seperation of two charges forming dipole , epsilon_0 = permittivity of free space by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Knowledge Check
- Question 1 - Select One
Electric field intensity (E) due to an electric dipole varies with distance (r ) from the point of the center of dipole as :
A1rand1r2B1r2and1rC1r3and1r3D1r3and1r2
Electric potential at any point in equatorial plane of a dipole is ………. .
View SolutionThe electric field at a point at a distance r from an electric dipole is proportional to ......
View SolutionCan the electric field by a small dipole be zero at a finite distance from electric dipole ?
View SolutionA point negative charge -Q is placed at a distance r from a dipole with dipole moment P in the xy plane as shown in fig. The x-component of force acting on the charge-Q is
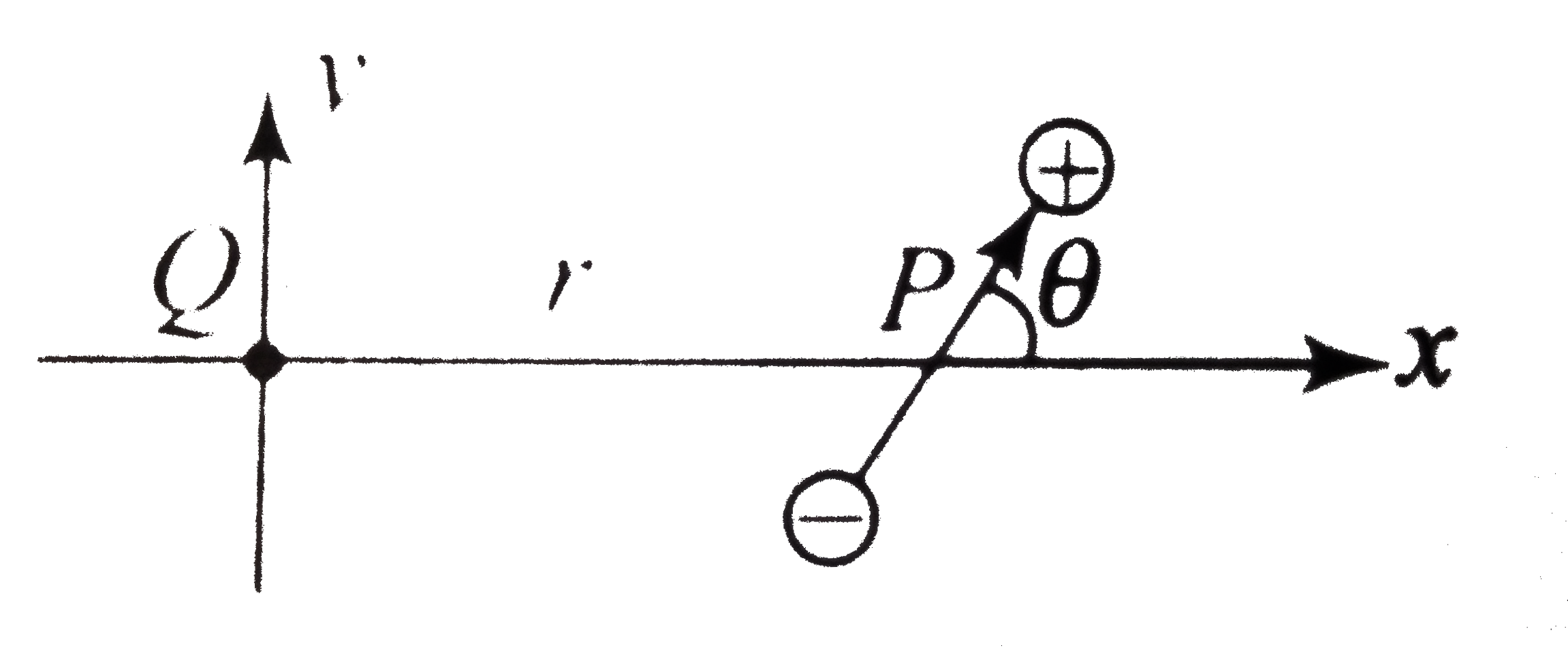
View SolutionAn electric dipole is kept on the axis of a uniformly charged ring at distance from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View SolutionTwo charges +20μCand−20μC are held 1cm apart. Calculate the electric field at a point on the equatorial line at a distance of 50cm from the center of the dipole.
View Solution(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.View Solution