In how many ways can a team of 6 horses be selected out of a stud of 16, so that there shall always be three out of A B C A B C, but never A A, B B or C C together a. b. c. d.
720
840
960
1260
The correct Answer is:C
16 horses=10 horses+(A,B,C,D,E,F)
The number of ways(Number of ways of ways of choosing out of A,B,C,D,E,F, so that AD,BE and CD are not together)
(One from each of pairs AD,BE,CF)
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (More Than One Correct Option Type Questions)10videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Passage Based Questions)15videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise For Session 75videos
PERMUTATIONS AND COMBINATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PARABOLAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)36videos
PARABOLA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)54videos
PROBABILITY
Similar Questions
In how many ways can a team of 11 players be formed out of 25 players, if 6 out of them are always to be included and 5 always to be excluded a. 2020 b. 2002 c. 2008 d. 8002
View SolutionIn how many ways can the 7 letters A, B, C, D, E, F, and G be arranged so that C and E are never together?
View SolutionThere are 6 students A,B,C,D,E,F. In how many ways can they be seated in a line so that C and D do not sit together?
View SolutionGive an example of three matrices A, B, C such that AB=AC but B≠C .
View SolutionGive an example of three matrices A, B, C such that AB=AC but B≠C .
View SolutionThere are 6 students A,B,C,D,E,F. In how many ways can a committee of 4 be formed so as to always include C?
View SolutionIn a ABC, BD and CE are the altitudes. Prove that ADB and AEC are similar. Is CDB~BEC ?
View SolutionThere are 6 students A,B,C,D,E,F. In hoiw many ways can a committee of 4 be formed so as to always include C but exclude E?
View SolutionSelect the correct labelling out of a, b c and d of mitochondrian
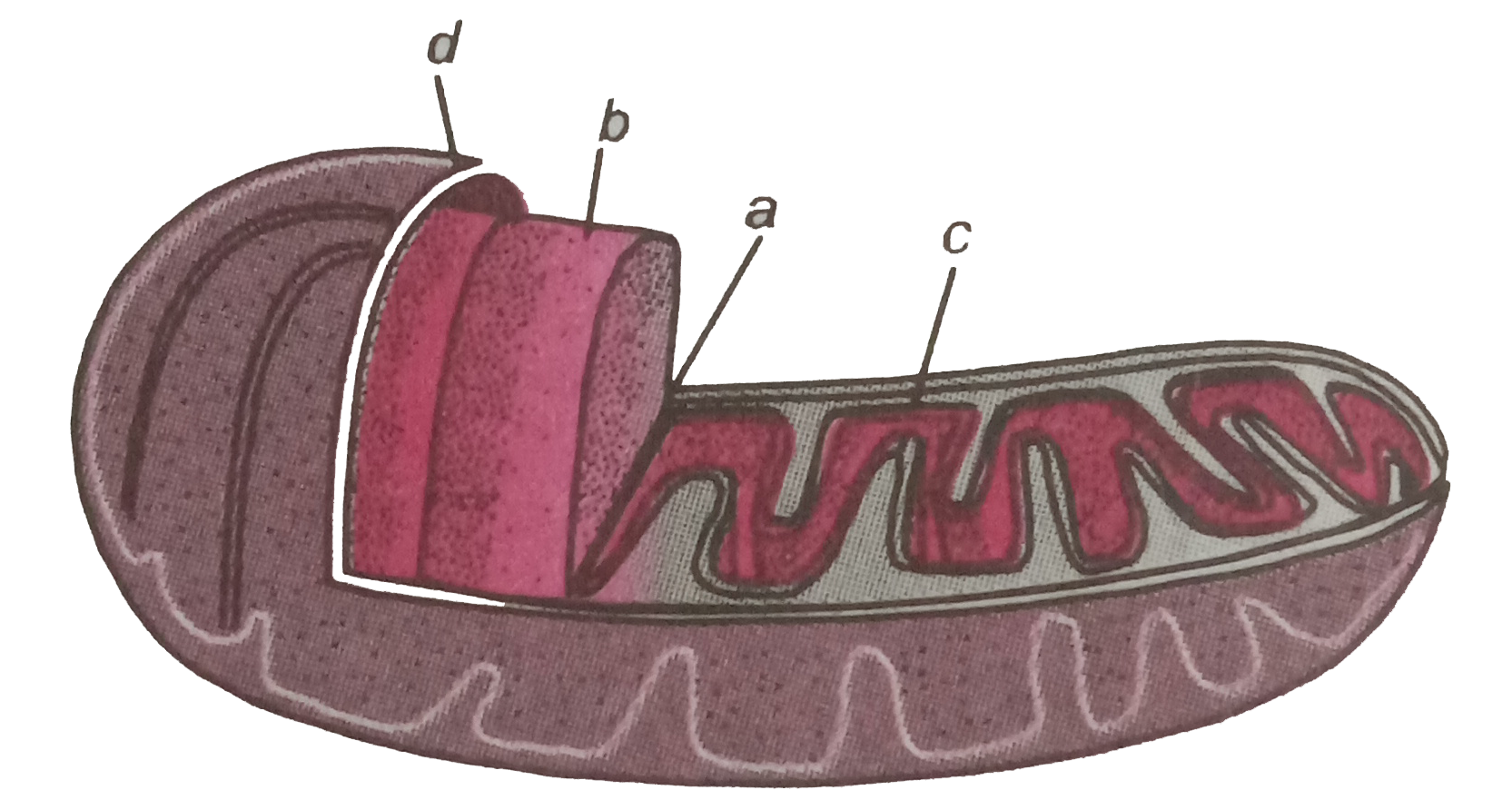 View Solution
View SolutionA person wants to go from station A to station C via station b. There are three routes from A to B four routes from B to C. In how many ways can he travel from A to C?
View Solution

