In a regular hexagon ABCDEF,¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=k¯¯¯¯¯¯AD then k is equal to
To find the value of k in the equation ¯AB+¯AC+¯AD+¯AE+¯AF=k¯AD for a regular hexagon ABCDEF, we will follow these steps:
Step 1: Understand the Geometry of the Hexagon
A regular hexagon can be divided into six equal segments. Each side of the hexagon is of equal length, which we will denote as L.
Step 2: Position Vectors
Let the position vector of point A be the origin, i.e., →A=→0. The position vectors of the other points can be represented as follows:
- →B=L (along the x-axis)
- →C=L(12,√32)
- →D=L(−12,√32)
- →E=−L (along the negative x-axis)
- →F=L(−12,−√32)
Step 3: Calculate Each Vector
Now we calculate each vector from point A:
- ¯AB=→B−→A=L
- ¯AC=→C−→A=L(12,√32)
- ¯AD=→D−→A=L(−12,√32)
- ¯AE=→E−→A=−L
- ¯AF=→F−→A=L(−12,−√32)
Step 4: Sum the Vectors
Now we sum these vectors:
¯AB+¯AC+¯AD+¯AE+¯AF=L+L(12,√32)+L(−12,√32)−L+L(−12,−√32)
Step 5: Simplify the Sum
Combining the vectors:
- The x-components:
L+L2−L2−L−L2=−L2
- The y-components:
0+L√32+L√32+0−L√32=L√32
Thus, the resulting vector is:
¯AB+¯AC+¯AD+¯AE+¯AF=(−L2,L√32)
Step 6: Express in terms of ¯AD
Now we need to express this sum in terms of ¯AD:
¯AD=L(−12,√32)
Thus, we can see that:
¯AB+¯AC+¯AD+¯AE+¯AF=3¯AD
Step 7: Conclusion
From the equation:
¯AB+¯AC+¯AD+¯AE+¯AF=k¯AD
we find that k=3.
Final Answer
Therefore, k is equal to 3.
---
A regular hexagon can be divided into six equal segments. Each side of the hexagon is of equal length, which we will denote as L.
Let the position vector of point A be the origin, i.e., →A=→0. The position vectors of the other points can be represented as follows:
- →B=L (along the x-axis)
- →C=L(12,√32)
- →D=L(−12,√32)
- →E=−L (along the negative x-axis)
- →F=L(−12,−√32)
Now we calculate each vector from point A:
- ¯AB=→B−→A=L
- ¯AC=→C−→A=L(12,√32)
- ¯AD=→D−→A=L(−12,√32)
- ¯AE=→E−→A=−L
- ¯AF=→F−→A=L(−12,−√32)
Now we sum these vectors:
¯AB+¯AC+¯AD+¯AE+¯AF=L+L(12,√32)+L(−12,√32)−L+L(−12,−√32)
Combining the vectors:
- The x-components:
L+L2−L2−L−L2=−L2
- The y-components:
0+L√32+L√32+0−L√32=L√32
¯AB+¯AC+¯AD+¯AE+¯AF=(−L2,L√32)
Now we need to express this sum in terms of ¯AD:
¯AD=L(−12,√32)
Thus, we can see that:
¯AB+¯AC+¯AD+¯AE+¯AF=3¯AD
From the equation:
¯AB+¯AC+¯AD+¯AE+¯AF=k¯AD
we find that k=3.
Therefore, k is equal to 3.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 3
11 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - VECTOR ALGEBRA EXERCISES 1: Single Option Correct Type Questions
1 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
In the figure shown below ,¯¯¯¯¯¯BC and bar(EF)areparal≤landbar(AE ) = bar(FD ) . ifangle ABC is130 ^(@) and angle (BAE)is22^@,wˆisthemeasureofangle (AEF) ?
 A50∘B118∘C152∘D158∘
A50∘B118∘C152∘D158∘Triangle △ACE, shown in the figure below, is isosceles with base ¯¯¯¯¯¯AE. B lies on ¯¯¯¯¯¯AC and D lies on ¯¯¯¯¯¯CE . Segments ¯¯¯¯¯¯BE and ¯¯¯¯¯¯AD bisect ∠AEC and ∠CAE, respectively. Which one of the following angle congruences is necessarily true ?
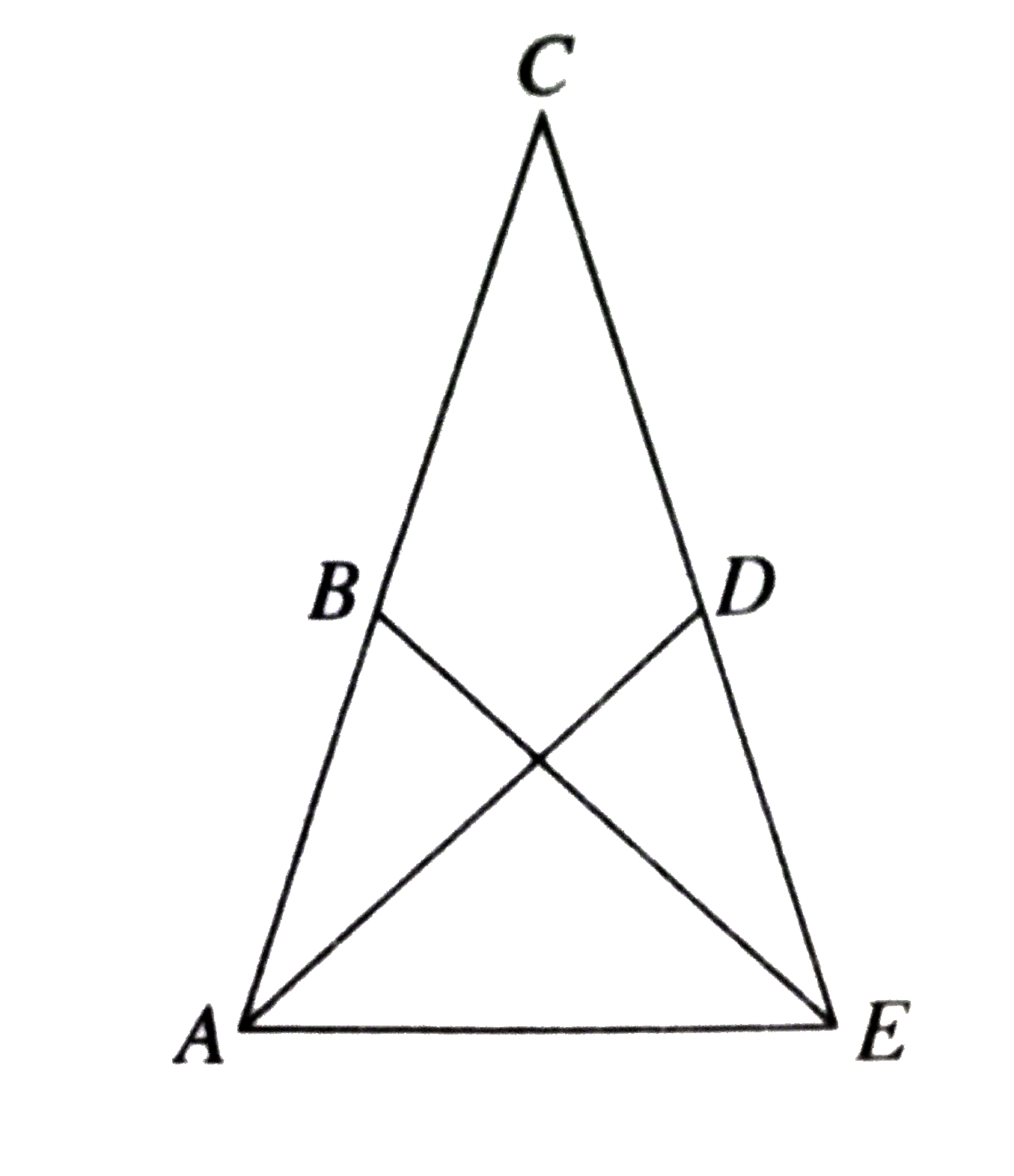 A∠CAE≅∠BECB∠CAD≅∠AECC∠CAE≅∠ACED∠BEC≅∠DAE
A∠CAE≅∠BECB∠CAD≅∠AECC∠CAE≅∠ACED∠BEC≅∠DAEIn the figure shown below, E and G lie on ¯¯¯¯¯¯AC, D and F lie on ¯¯¯¯¯¯AB,¯¯¯¯¯¯DEand¯¯¯¯¯¯FG are parallel to ¯¯¯¯¯¯BC, and the given lengths are in feet. What is the length of ¯¯¯¯¯¯AC, in feet?
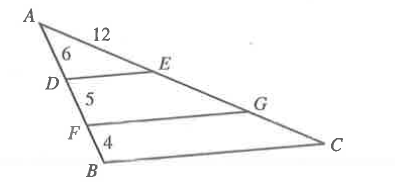 A9B18C21D30
A9B18C21D30
(¯a⋅¯i)2+(¯a⋅¯j)2+(¯a⋅¯k)2=
View SolutionIn the figure below , the circle with circle with center O is tangent to ¯¯¯¯¯¯AE,¯¯¯¯¯¯BD,and¯¯¯¯¯¯DE . The measure of angle ∠BDE is 75∘ and the maeasure of ∠DEA is 105∘
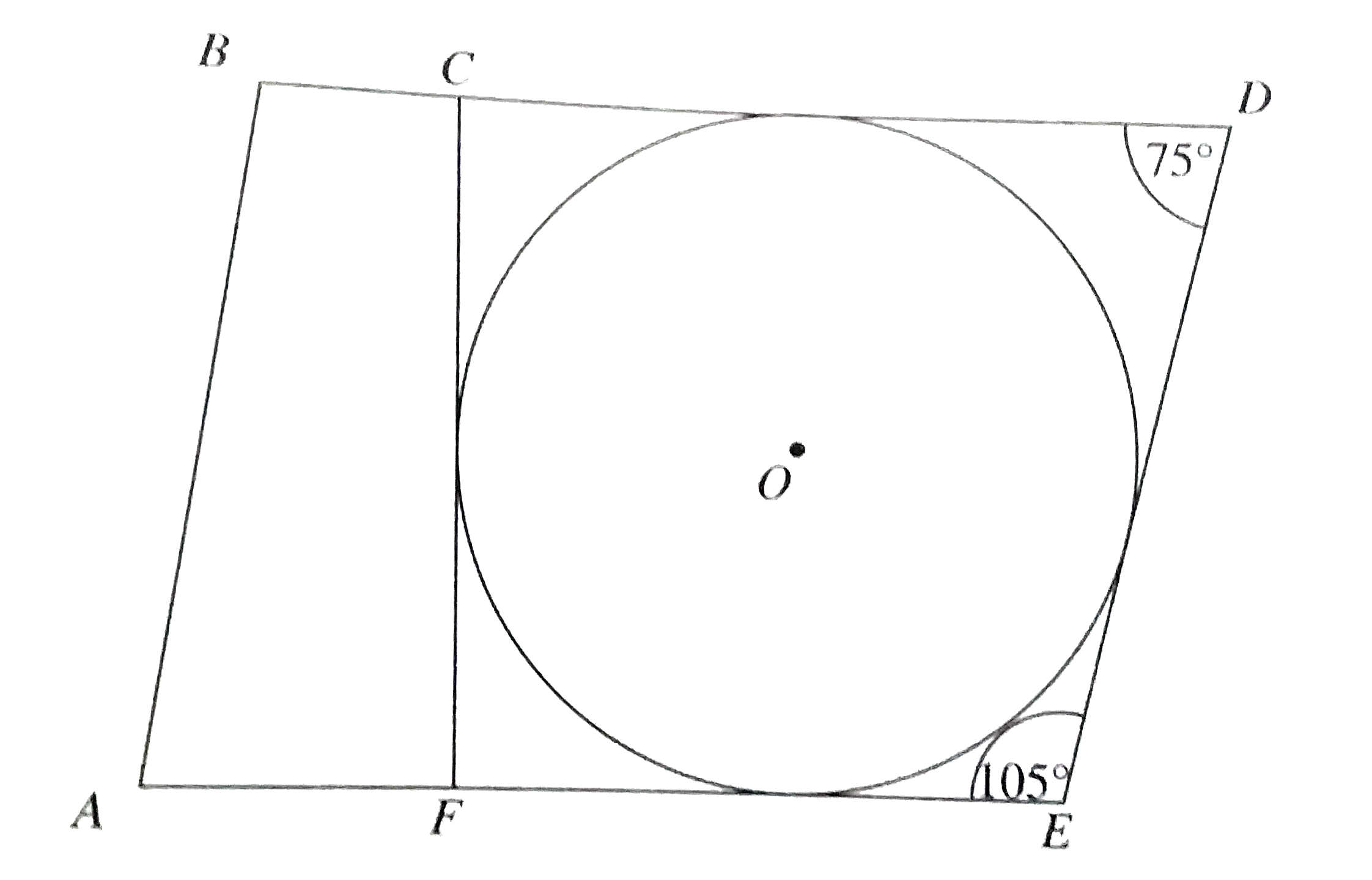
THe lines in which of the following pairs of lines are necessarily parallel ?
I.¯¯¯¯¯¯ABand¯¯¯¯¯¯DE
II.¯¯¯¯¯¯BDand¯¯¯¯¯¯AE
III.¯¯¯¯¯¯CFand¯¯¯¯¯¯DE
View SolutionIn the figure below, ¯¯¯¯¯¯AB≡¯¯¯¯¯¯ACand¯¯¯¯¯¯BC is 10 units long. What is the area, in square in square inches, of △ABC ?
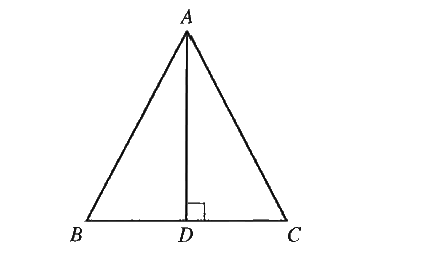
View SolutionIn the figure below, A, D, C and E are collinear . ¯¯¯¯¯¯AD,¯¯¯¯¯¯BD,and¯¯¯¯¯¯BC are all the same length, and the angle measure of ∠ABD is as marked. What is the degree measure of ∠BCE?
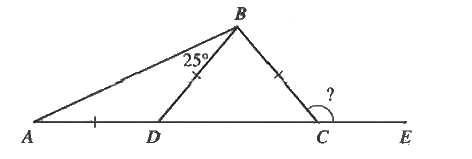
View SolutionIn △ACD below, B is on ¯¯¯¯¯¯AC, E is on ¯¯¯¯¯¯AD, the measure of ∠CAD is 28∘, and ¯¯¯¯¯¯AD is perpendicular to both ¯¯¯¯¯¯BE and ¯¯¯¯¯¯CD. What is the measure of ∠CBE?
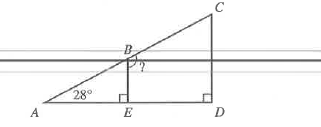
View Solution
