Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:OC.
7//3
4
The correct Answer is:B
To solve the problem, we need to find the ratio OX:OC in the pentagon OABCD where OA∥CB and OD∥AB. Given the ratios OA:CB=2:1 and OD:AB=1:3, we can use vector algebra to find the required ratio.
Step 1: Define the Position Vectors
Let:
- →O=→0 (the origin)
- Let →A=→a
- Let →B=→b
- Let →C=→c
- Let →D=→d
Step 2: Express the Vectors Based on the Given Ratios
From the ratio OA:CB=2:1:
→A−→O=2(→C−→B)⟹→a=2(→c−→b)⟹→a=2→c−2→b
From the ratio OD:AB=1:3:
3(→D−→O)=→B−→A⟹3→d=→b−→a⟹→d=13(→b−→a)
Step 3: Substitute →a into the Equation for →d
Substituting →a=2→c−2→b into →d:
→d=13(→b−(2→c−2→b))=13(→b−2→c+2→b)=13(3→b−2→c)=→b−23→c
Step 4: Express the Diagonals OC and AD
We need to find the intersection point X of the diagonals OC and AD. Let:
- OX:XA=λ:1
- AX:XD=μ:1
Using the section formula, the position vector of X from OC is:
→X=λ→c+1⋅→0λ+1=λ→cλ+1
From AD:
→X=μ→d+1⋅→aμ+1
Step 5: Equate the Two Expressions for →X
Equating the two expressions for →X:
λ→cλ+1=μ(→b−23→c)+→aμ+1
Step 6: Substitute →a and →d into the Equation
Substituting →a=2→c−2→b:
λ→cλ+1=μ(→b−23→c)+(2→c−2→b)μ+1
Step 7: Solve for λ and μ
After equating coefficients and simplifying, we find:
1. Coefficient of →c gives us one equation.
2. Coefficient of →b gives us another equation.
Step 8: Find the Ratio OX:OC
After solving the equations, we find λ and μ. The ratio OX:OC can be expressed as:
OX:OC=λλ+1
Final Result
After calculating, we find:
OX:OC=2:5
Let:
- →O=→0 (the origin)
- Let →A=→a
- Let →B=→b
- Let →C=→c
- Let →D=→d
From the ratio OA:CB=2:1:
→A−→O=2(→C−→B)⟹→a=2(→c−→b)⟹→a=2→c−2→b
3(→D−→O)=→B−→A⟹3→d=→b−→a⟹→d=13(→b−→a)
Substituting →a=2→c−2→b into →d:
→d=13(→b−(2→c−2→b))=13(→b−2→c+2→b)=13(3→b−2→c)=→b−23→c
We need to find the intersection point X of the diagonals OC and AD. Let:
- OX:XA=λ:1
- AX:XD=μ:1
→X=λ→c+1⋅→0λ+1=λ→cλ+1
→X=μ→d+1⋅→aμ+1
Equating the two expressions for →X:
λ→cλ+1=μ(→b−23→c)+→aμ+1
Substituting →a=2→c−2→b:
λ→cλ+1=μ(→b−23→c)+(2→c−2→b)μ+1
After equating coefficients and simplifying, we find:
1. Coefficient of →c gives us one equation.
2. Coefficient of →b gives us another equation.
After solving the equations, we find λ and μ. The ratio OX:OC can be expressed as:
OX:OC=λλ+1
After calculating, we find:
OX:OC=2:5
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Matching Type Questions)
1 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Single Integer Answer Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal AC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal BD.
View SolutionTwo sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View SolutionThe sides AB and AD of a parallelogram ABCD are 2x−y+1=0andx+3y−10=0 respectively and C is the point (−1,−2). Find the equation of the diagonals AC.
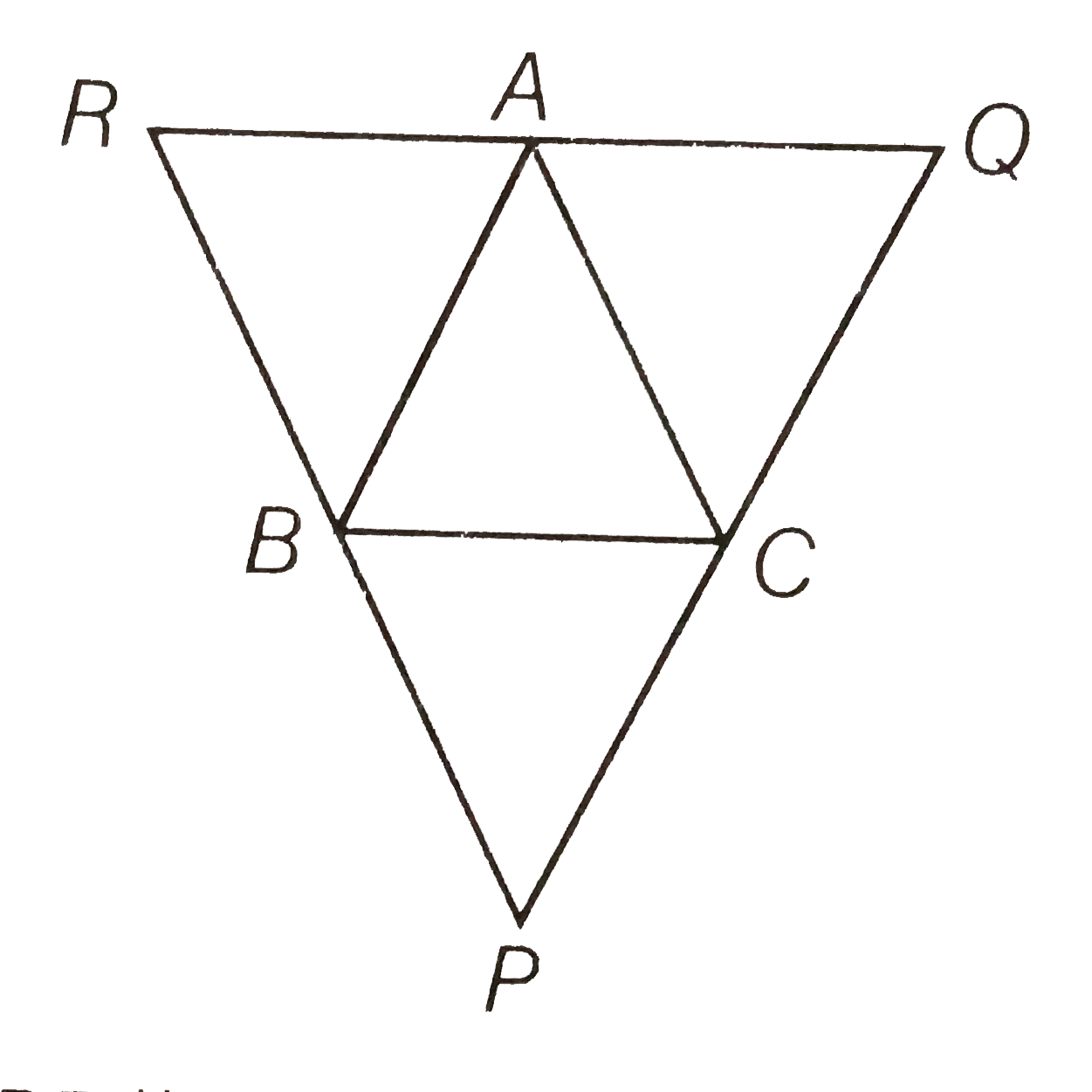
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
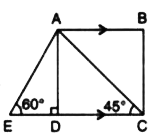
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(i) AB
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
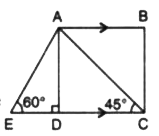
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(iii) AE
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
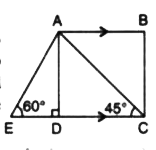
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(ii) AC
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View Solution
