If u,v and w is a linearly independent system of vectors, examine the system p,q and r, where p=(cosa)u+(cosb)v+(cosc)w q=(sina)u+(sinb)v+(sinc)w r=sin(x+a)u+sin(x+b)v+sin(x+c)w for linearly dependent.
To determine whether the vectors p,q, and r are linearly dependent given that u,v, and w are linearly independent, we will analyze the linear combination of these vectors.
1. Define the Vectors:
We have:
p=cosa⋅u+cosb⋅v+cosc⋅w
q=sina⋅u+sinb⋅v+sinc⋅w
r=sin(x+a)⋅u+sin(x+b)⋅v+sin(x+c)⋅w
2. Set Up the Matrix:
To check for linear dependence, we can form a matrix with p,q, and r as its rows or columns. We will use the following matrix:
A=⎡⎢⎣cosacosbcoscsinasinbsincsin(x+a)sin(x+b)sin(x+c)⎤⎥⎦
3. Calculate the Determinant:
We need to find the determinant of matrix A. If the determinant is zero, then the vectors are linearly dependent.
det(A)=∣∣
∣∣cosacosbcoscsinasinbsincsin(x+a)sin(x+b)sin(x+c)∣∣
∣∣
4. Use Trigonometric Identities:
We can express sin(x+a), sin(x+b), and sin(x+c) using the angle addition formula:
sin(x+a)=sinxcosa+cosxsina
Similarly for b and c.
5. Substitute into the Matrix:
Substitute the expressions from the angle addition formula into the third row of the matrix:
A=⎡⎢⎣cosacosbcoscsinasinbsincsinxcosa+cosxsinasinxcosb+cosxsinbsinxcosc+cosxsinc⎤⎥⎦
6. Row Operations:
Perform row operations to simplify the matrix. We can subtract the first row multiplied by sinx and the second row multiplied by cosx from the third row:
R3→R3−sinx⋅R1−cosx⋅R2
This will lead to a new third row that is a linear combination of the first two rows.
7. Check for Linear Dependence:
After performing the row operation, if the third row becomes a row of zeros, then the determinant will be zero, indicating that the vectors p,q,r are linearly dependent.
8. Conclusion:
Since we have shown that the determinant of the matrix formed by p,q,r is zero, we conclude that the vectors p,q,r are linearly dependent.
Final Answer:
Therefore, the vectors p,q,r are linearly dependent.
---
We have:
p=cosa⋅u+cosb⋅v+cosc⋅w
q=sina⋅u+sinb⋅v+sinc⋅w
r=sin(x+a)⋅u+sin(x+b)⋅v+sin(x+c)⋅w
To check for linear dependence, we can form a matrix with p,q, and r as its rows or columns. We will use the following matrix:
A=⎡⎢⎣cosacosbcoscsinasinbsincsin(x+a)sin(x+b)sin(x+c)⎤⎥⎦
We need to find the determinant of matrix A. If the determinant is zero, then the vectors are linearly dependent.
det(A)=∣∣
∣∣cosacosbcoscsinasinbsincsin(x+a)sin(x+b)sin(x+c)∣∣
∣∣
We can express sin(x+a), sin(x+b), and sin(x+c) using the angle addition formula:
sin(x+a)=sinxcosa+cosxsina
Similarly for b and c.
Substitute the expressions from the angle addition formula into the third row of the matrix:
A=⎡⎢⎣cosacosbcoscsinasinbsincsinxcosa+cosxsinasinxcosb+cosxsinbsinxcosc+cosxsinc⎤⎥⎦
Perform row operations to simplify the matrix. We can subtract the first row multiplied by sinx and the second row multiplied by cosx from the third row:
R3→R3−sinx⋅R1−cosx⋅R2
This will lead to a new third row that is a linear combination of the first two rows.
After performing the row operation, if the third row becomes a row of zeros, then the determinant will be zero, indicating that the vectors p,q,r are linearly dependent.
Since we have shown that the determinant of the matrix formed by p,q,r is zero, we conclude that the vectors p,q,r are linearly dependent.
Therefore, the vectors p,q,r are linearly dependent.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)9videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Single Integer Answer Type Questions)7videos
VECTOR ALGEBRA
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)19videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
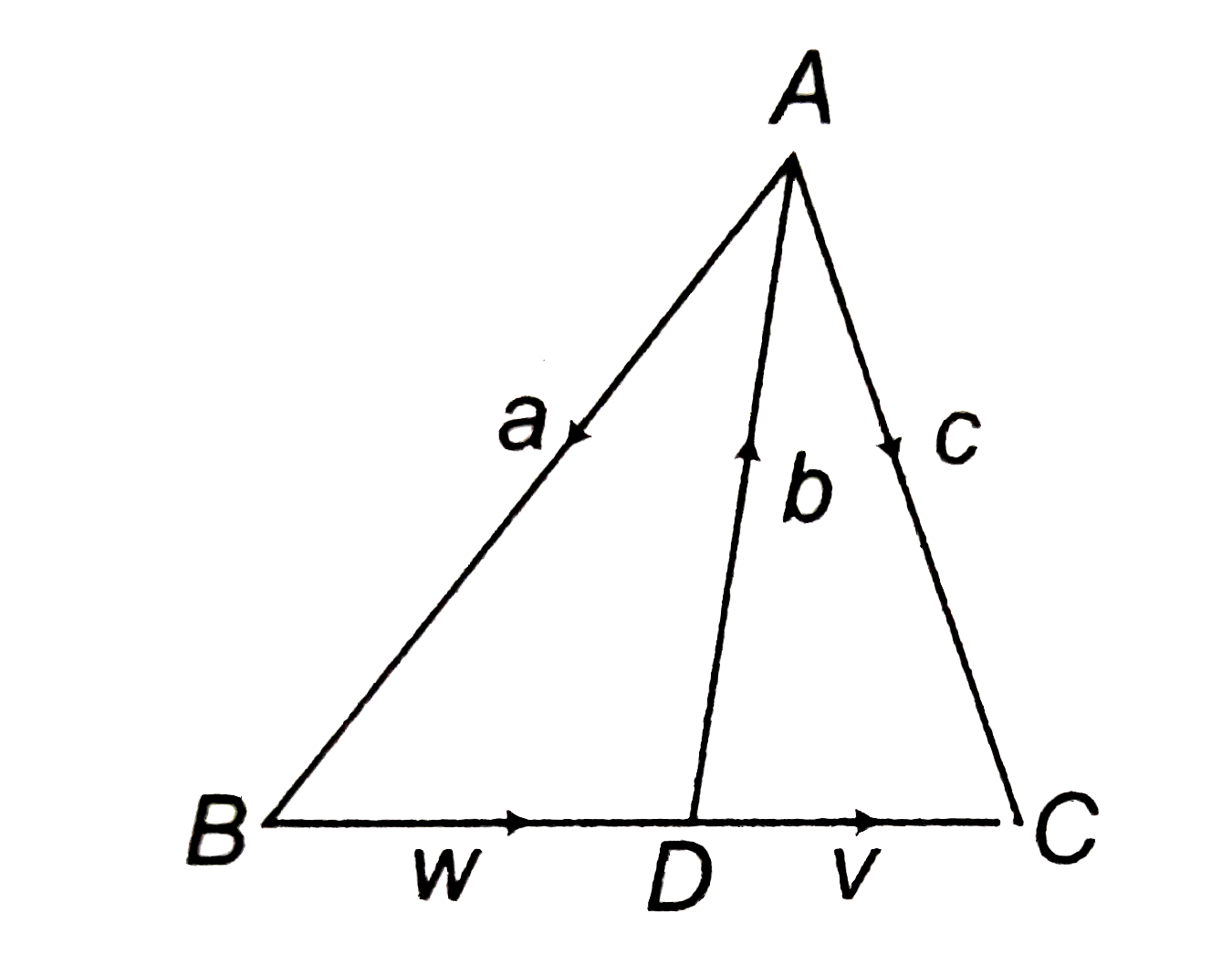
In the figure, a vectors x satisfies the equation x+w=v. then, x is equal to
 View Solution
View SolutionIf a ,b,c, and u,v,w are complex numbers representing the vertices of two triangle such that they are similar, then prove that a−ca−b=u−wu−v
View SolutionAssertion :- For an isolated system q is zero.
Reason :- In an isolated system change in U and V is zero.View SolutionIf →u,→vand→w are three non-cop0lanar vectors, then prove that (→u+→v−→w). [(→u−→v)×(→v−→w)]= →u. (→v×→w)
View SolutionIf the roots of the equation x3−10x+11=0 are u, v, and w, then the value of 3cosec2(tan−1u+tan−1v+tan−1w is ____
View Solution→u,→v and →w are three non-coplanar unit vecrtors and α,β and γ are the angles between→u and →v,→vand →w,and→w and →u, respectively, and →x,→y and →z are unit vectors along the bisectors of the angles α,βandγ , respectively. Prove that [→x×→y→y×→z→z×→x]=116[→u→v→w]2sec2(α2)sec2(β2)sec2(γ2).
View SolutionIf →u,→vand→w are three non-coplanar vectors, then prove that (→u+→v−→w).[[(→u−→v)×(→v−→w)]]=→u.→v×→w
View SolutionLet ˆu,ˆvandˆw are three unit vectors, the angle between ˆuandˆv is twice that of the angle between ˆuandˆwandˆvandˆw, then [ˆuˆvˆw] is equal to
View SolutionLet u,v,w be rela numbers in geometric progression such that u>v>w. Suppose u40=vn=w60. Find the value of n .
View SolutionIf a,b,c and u,v,w are the complex numbers representing the vertices of two triangles such that (c=(1−r)a+rb and w=(1−r)u+rv, where r is a complex number, then the two triangles (a)have the same area (b) are similar (c)are congruent (d) None of these
View Solution

