(A) a1,a2,...... are in AP.
a1+a4+a7+a14+a17+a20=165 [In an AP, sum of the terms equidistant from the 1st and last is equal to sum of 1st and last terms]
⇒3(a1+a20)=165
⇒a1+a1+19d=55
d is the common difference of AP.
2a1+19d=55 .......(i)
Now, α=a2+a6+a15+a19
α=2(a2+a19)
α=2(a1+d+a1+18d)
α=2(2a1+19d) ......(ii)
and β=2(a9+a12)−(a3+a18)
β=2(a1+8d+a1+11d)−(a1+2d+a1+17d)
β=2(2a1+19d)−(2a1+19d)
β=2a1+19d ......(iii)
From Eqs. (i) and (iii), we get
α=2β
From Eqs. (i),(ii) and (iii), we get
α+2β=4(2a1+19d)=4(55)=220 [ from Eq.(i)]
α+β=3(2a1+19d)
=3×55=165=15×11=15μ, where μ∈I
α−β=2a1+19d
=55=5×11=5λ, where λ∈I.
(B) a1,a2,...... are in AP.
a1+a5+a10+a15+a20+a24=195
3(a1+a24)=195
⇒a1+a24=65 .....(i)
⇒2a1+23d=65
Now, α=a2+a7+a18+a23
=2(a2+a23)=2(2a1+23d)
α=130 [ fromEq. (i)]
β=2(a2+a22)−(a8+a17)
=2(2a2+23d)−(2a2+23d)
=130−65=65
Then, α=2β
α+2β=130+130=260
α+β=195=15×13=15μ, where μ=13
and α−β=130−65=65
=5×13=5λ, where λ=13.
(C ) a1,a2,.... are in AP.
a1+a7+a10+a21+a24+a30=225
3(a1+a30)=225
2a1+29d=75 ........(i)
Now, α=a2+a7+a24+a29
α=4a1+58d=2(2a1+29d)
2×75=150
α=150 .......(ii)
and β=2(a10+a21)−(a3+a28)
=2(2a1+29d)−(2a1+29d)=150−75
β=75 ......(iii)
Then, α=2β
α+2β=150+150=300 and α−β=150−75=75
=5×15=5λ, where λ=15
and α+β=150+75=225=15×15=15μ, where μ=15.
Topper's Solved these Questions
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Subjective Type Questions)
24 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Matching Type Questions)
3 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
- SETS, RELATIONS AND FUNCTIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - SETS, RELATIONS AND FUNCTIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
12 Videos
Similar Questions
Statement 1 4,8,16, are in GP and 12,16,24 are in HP.
Statement 2 If middle term is added in three consecutive terms of a GP, resultant will be in HP.
View SolutionThe pth, (2p)th and (4p)th terms of an AP, are in GP, then find the common ratio of GP.
View SolutionMatch the following Column I to Column II

View SolutionIn a triangle XYZ, let x, y, z be the lengths of sides opposite to the angles X, Y, Z, respectively, and 2s = x + y + z. If s−x4=s−y3=s−z2 of incircle of the triangle XYZ is 8π3
View SolutionLet R={(3,3),(6,6),(9,9),(6,12),(3,9),(3,12),(12,12),(3,6)} is a relation on set A={3,6,9,12} then R is a) an equivalence relation b) reflexive and symmetric only c) reflexive and transitive only d) reflexive only
View SolutionHow many lines of symmetry does the above figure have ?
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
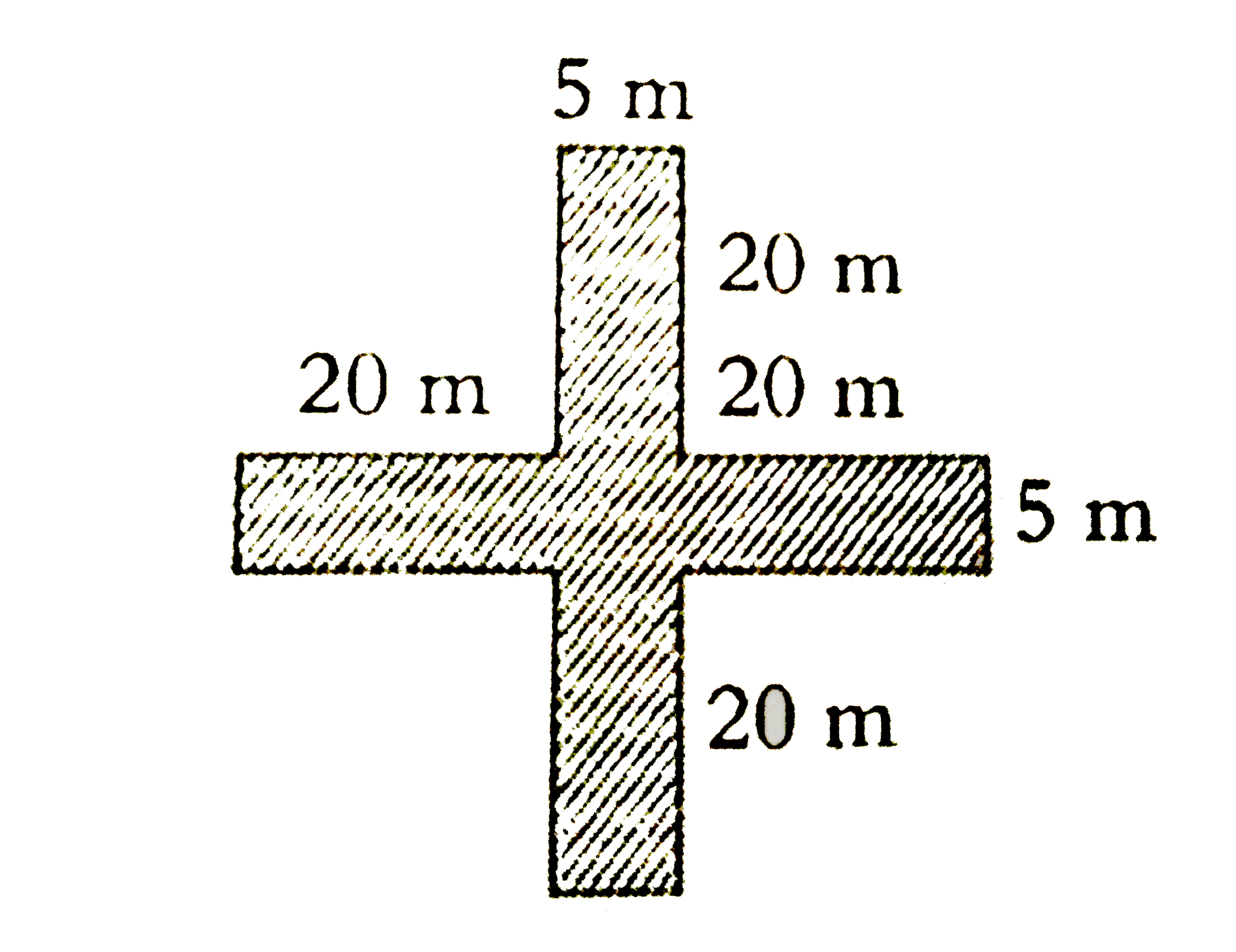
View SolutionThe area of the shaded part in the figure given below is ______.
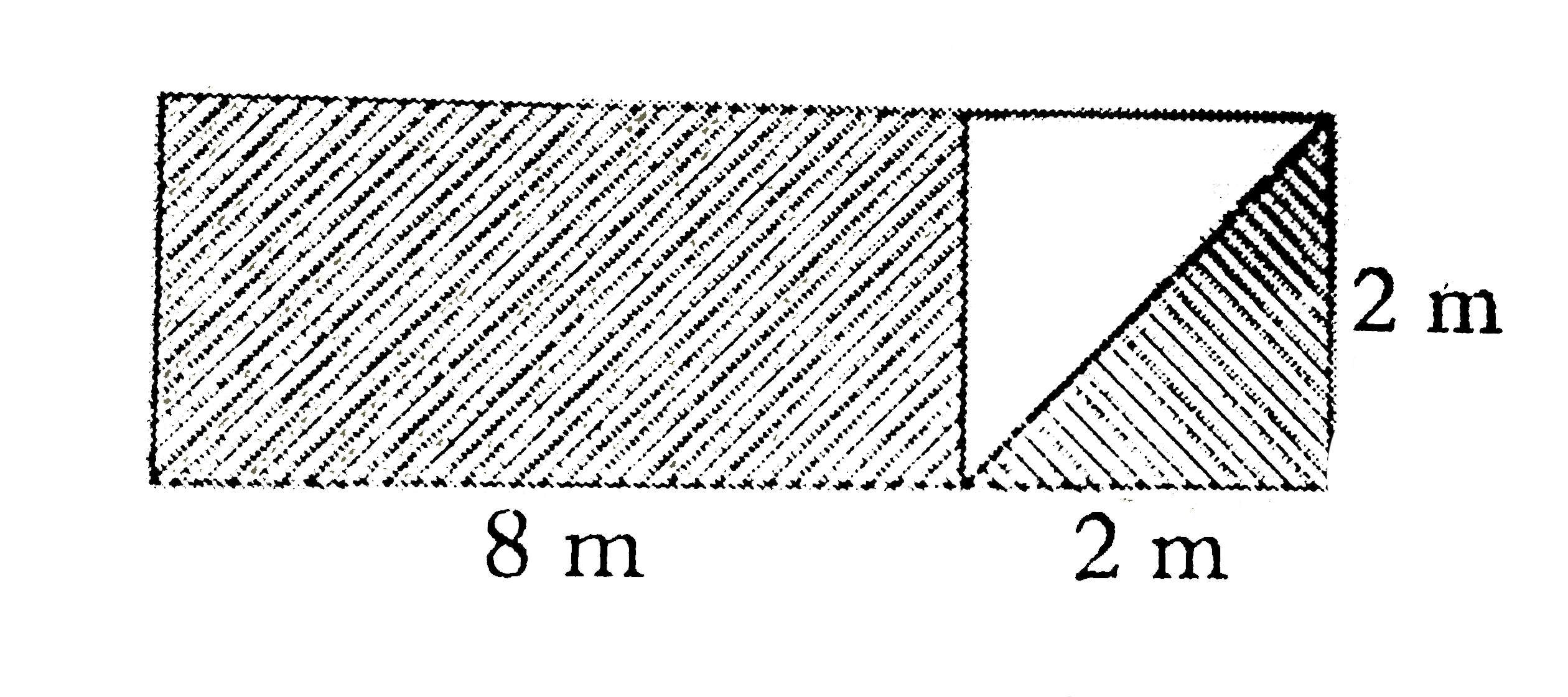
View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View Solution


