Consider the following function f whose graph is given below.
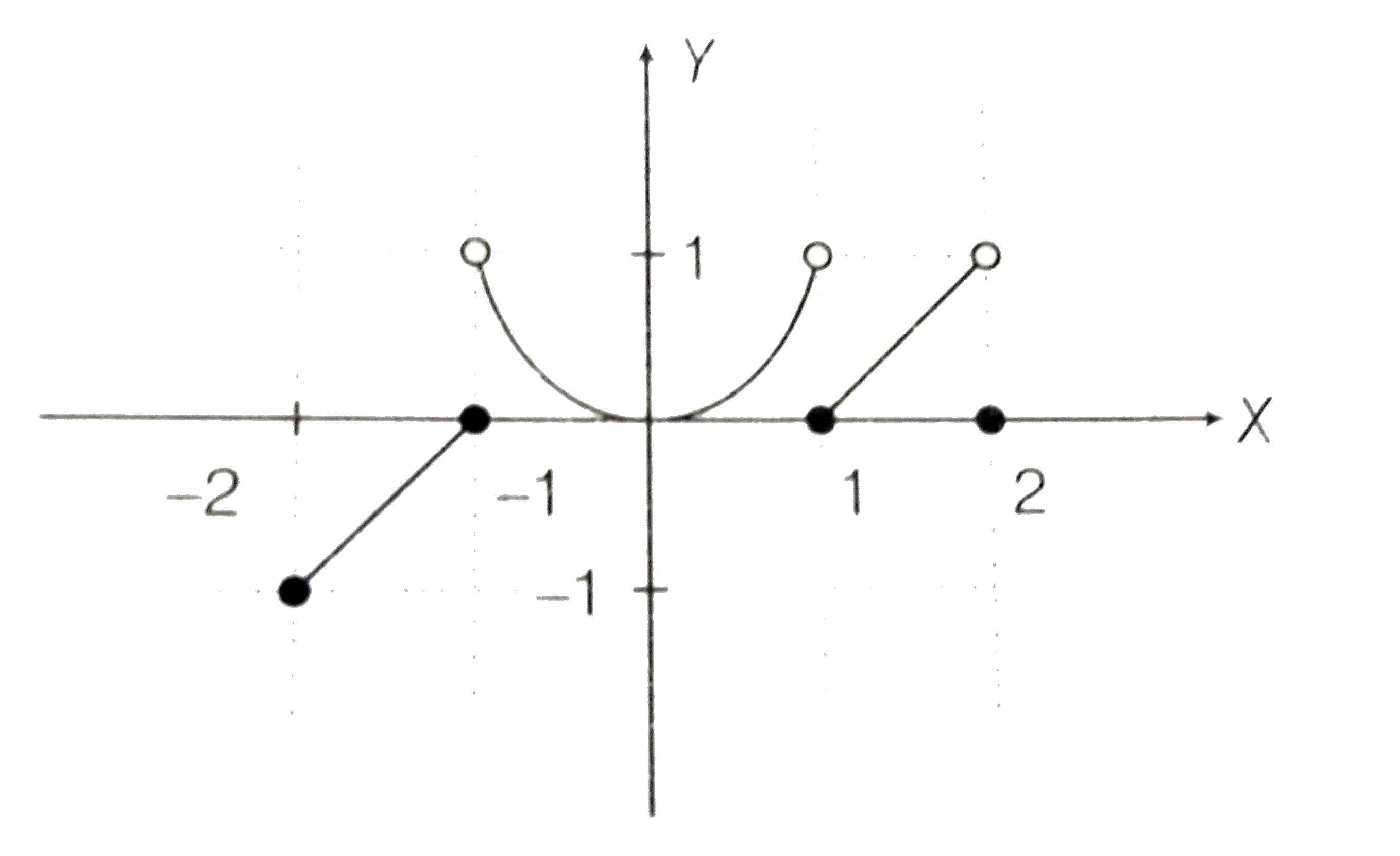
Step by step video & image solution for Consider the following function f whose graph is given below. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise For Session 3
16 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise For Session 4
12 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise For Session 1
8 Videos
- FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - FUNCTION EXERCISE 8:Questions Asked in Previous 10 Years Exams
1 Videos
- HYPERBOLABOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams
3 Videos
Similar Questions
Which of the following is a function whose graph is symmetrical about the origin ?
View SolutionObserve the bar graph given below :

Read the bar graph carefully and answer the following questions :
What information is given by the bar graph?
View SolutionA function whose graph is symmetrical about y-axis is
View SolutionGiven below is a bar graph showing the heights of six mountain peaks.
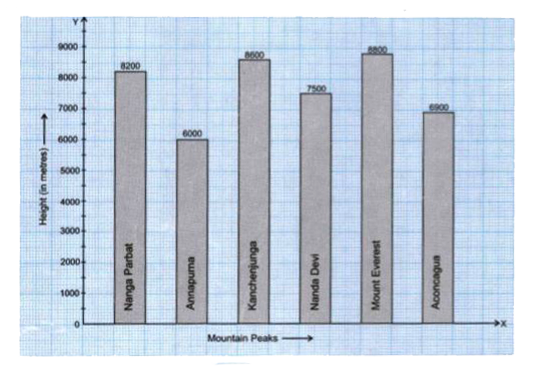
Read the above bar diagram and answer the following questions :
what is information given in the graph
View SolutionConsider the following graphs of the functions. Check each for the extrema at x=a
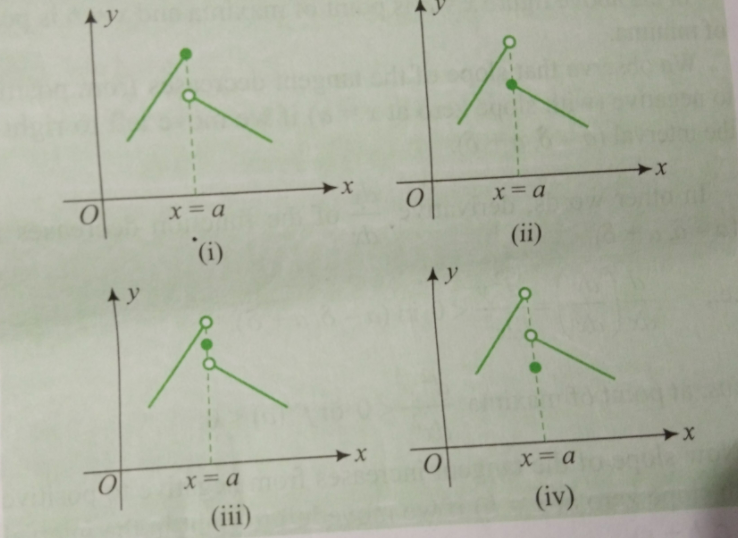
View SolutionWhich one of the following function best represents the graphs as shown below?

View SolutionConsider the reaction given below :
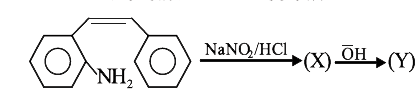
View SolutionObserve the graph given below and answer the following questions:

At two places, the graph is parallel to the x-axis. What does this mean?
View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?

(a)limx→1f(x) does not exist.
(b)limx→2f(x) does not exist.
(c)limx→3f(x)=3.
(d)limx→1.99f(x)exists.
View SolutionA function whose graph is symmetrical in opposite quadrants is
View Solution
