A, B, C and D are four points in space. Using vector methods, prove that AC2+BD2+AC2+BC2≥AB2+CD2 what is the implication of the sign of equality.
AB2+CD2
1AB2−1CD2
1CD2−1AB2
None of these
The correct Answer is:(a)
To prove the inequality AC2+BD2+AC2+BC2≥AB2+CD2 using vector methods, we can follow these steps:
Step 1: Define Position Vectors
Let the position vectors of points A, B, C, and D be represented as:
- →a for point A
- →b for point B
- →c for point C
- →d for point D
Step 2: Express Squared Distances
We can express the squared distances in terms of the position vectors:
- AC2=|→c−→a|2=(→c−→a)⋅(→c−→a)=|→c|2−2→a⋅→c+|→a|2
- BD2=|→d−→b|2=(→d−→b)⋅(→d−→b)=|→d|2−2→b⋅→d+|→b|2
- BC2=|→c−→b|2=|→c|2−2→b⋅→c+|→b|2
- AB2=|→b−→a|2=|→b|2−2→a⋅→b+|→a|2
- CD2=|→d−→c|2=|→d|2−2→c⋅→d+|→c|2
Step 3: Substitute and Rearrange
Now, substitute these expressions into the inequality:
AC2+BD2+AC2+BC2≥AB2+CD2
This becomes:
(|→c|2−2→a⋅→c+|→a|2)+(|→d|2−2→b⋅→d+|→b|2)+(|→c|2−2→b⋅→c+|→b|2)≥(|→b|2−2→a⋅→b+|→a|2)+(|→d|2−2→c⋅→d+|→c|2)
Step 4: Combine Like Terms
Combine all the terms on both sides:
- Left-hand side (LHS):
2|→c|2+2|→b|2+|→d|2−2→a⋅→c−2→b⋅→d−2→b⋅→c
- Right-hand side (RHS):
|→b|2+|→a|2+|→d|2+|→c|2−2→a⋅→b−2→c⋅→d
Step 5: Rearranging the Inequality
Now rearranging gives:
|→c|2+|→b|2−2→b⋅→c−2→a⋅→c+2→a⋅→b+2→c⋅→d≥0
Step 6: Recognizing the Square
This expression can be recognized as a squared term:
|→a+→b−→c−→d|2≥0
This is always true since the square of a vector's magnitude is always non-negative.
Step 7: Implication of Equality
The equality holds when:
→a+→b=→c+→d
This implies that the points A, B, C, and D are coplanar and lie on a straight line.
Let the position vectors of points A, B, C, and D be represented as:
- →a for point A
- →b for point B
- →c for point C
- →d for point D
We can express the squared distances in terms of the position vectors:
- AC2=|→c−→a|2=(→c−→a)⋅(→c−→a)=|→c|2−2→a⋅→c+|→a|2
- BD2=|→d−→b|2=(→d−→b)⋅(→d−→b)=|→d|2−2→b⋅→d+|→b|2
- BC2=|→c−→b|2=|→c|2−2→b⋅→c+|→b|2
- AB2=|→b−→a|2=|→b|2−2→a⋅→b+|→a|2
- CD2=|→d−→c|2=|→d|2−2→c⋅→d+|→c|2
Now, substitute these expressions into the inequality:
AC2+BD2+AC2+BC2≥AB2+CD2
This becomes:
(|→c|2−2→a⋅→c+|→a|2)+(|→d|2−2→b⋅→d+|→b|2)+(|→c|2−2→b⋅→c+|→b|2)≥(|→b|2−2→a⋅→b+|→a|2)+(|→d|2−2→c⋅→d+|→c|2)
Combine all the terms on both sides:
- Left-hand side (LHS):
2|→c|2+2|→b|2+|→d|2−2→a⋅→c−2→b⋅→d−2→b⋅→c
- Right-hand side (RHS):
|→b|2+|→a|2+|→d|2+|→c|2−2→a⋅→b−2→c⋅→d
Now rearranging gives:
|→c|2+|→b|2−2→b⋅→c−2→a⋅→c+2→a⋅→b+2→c⋅→d≥0
This expression can be recognized as a squared term:
|→a+→b−→c−→d|2≥0
This is always true since the square of a vector's magnitude is always non-negative.
The equality holds when:
→a+→b=→c+→d
This implies that the points A, B, C, and D are coplanar and lie on a straight line.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (More Than One Correct Option Type Questions)28videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise (Statement I And Ii Type Questions)12videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Exercise For Session 47videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)35videos
THEORY OF EQUATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)12videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONS
Similar Questions
In a rhombus ABCD, prove that AC2+BD2=4AB2
View SolutionIn a rectangle ABCD, prove that : AC2+BD2=AB2+BC2+CD2+DA2.
View SolutionIn △ABC,∠A=60∘ prove that BC2=AB2+AC2−AB.AC
View SolutionUsing vector method prove that in any triangle ABC a2=b2+c2−2bccosA.
View SolutionIn any triangle ABC, prove that AB2+AC2=2(AD2+BD2) , where D is the midpoint of BC.
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
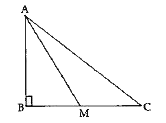 View Solution
View SolutionIn a quadrilateral ABCD, ∠A+∠D=90∘. Prove that
AC2+BD2=AD2+BC2View SolutionIf AD is the median of ABC, using vectors, prove that AB2+AC2=2(AD2+CD2).
View SolutionIn a quadrilateral ABCD ∠B=∠D=90∘ Prove that : 2AC2−BC2=AB2+AD2+DC2
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View Solution

