Show that the triangle, the coordinates of whose verticles are given by integers, can never be an equilateral triangle.
The correct Answer is:c=±b√3
To prove that a triangle with vertices at integer coordinates cannot be an equilateral triangle, we will analyze the area of the triangle using two different methods: one based on the coordinates of the vertices and the other based on the length of the sides.
1. Define the Vertices:
Let the vertices of the triangle be A(x1,y1), B(x2,y2), and C(x3,y3), where x1,y1,x2,y2,x3,y3 are all integers.
2. Area of the Triangle using Coordinates:
The area A of the triangle can be calculated using the formula:
A=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Since x1,y1,x2,y2,x3,y3 are integers, the expression inside the absolute value is an integer. Therefore, the area A is a half of an integer, which means A is a rational number.
3. Area of the Equilateral Triangle:
For an equilateral triangle with side length a, the area is given by:
A=√34a2
Here, a is the length of the side of the triangle. If the triangle has vertices with integer coordinates, then the side length a must also be a rational number (since the distance between two points with integer coordinates is a rational number).
4. Rational vs. Irrational:
Since a is rational, a2 is also rational. However, when we multiply a rational number a2 by the irrational number √3, the product √34a2 becomes irrational. Thus, the area of the equilateral triangle is irrational.
5. Conclusion:
We have shown that the area of a triangle with integer coordinates is rational, while the area of an equilateral triangle (with integer coordinates) is irrational. Therefore, it is impossible for a triangle with vertices at integer coordinates to be an equilateral triangle.
Let the vertices of the triangle be A(x1,y1), B(x2,y2), and C(x3,y3), where x1,y1,x2,y2,x3,y3 are all integers.
The area A of the triangle can be calculated using the formula:
A=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Since x1,y1,x2,y2,x3,y3 are integers, the expression inside the absolute value is an integer. Therefore, the area A is a half of an integer, which means A is a rational number.
For an equilateral triangle with side length a, the area is given by:
A=√34a2
Here, a is the length of the side of the triangle. If the triangle has vertices with integer coordinates, then the side length a must also be a rational number (since the distance between two points with integer coordinates is a rational number).
Since a is rational, a2 is also rational. However, when we multiply a rational number a2 by the irrational number √3, the product √34a2 becomes irrational. Thus, the area of the equilateral triangle is irrational.
We have shown that the area of a triangle with integer coordinates is rational, while the area of an equilateral triangle (with integer coordinates) is irrational. Therefore, it is impossible for a triangle with vertices at integer coordinates to be an equilateral triangle.
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Find all the angles of an equilateral triangle.
View SolutionProve that the coordinates of the vertices of an equilateral triangle can not all be rational.
View SolutionShow that the equation of the circle with centre at origin and passing through the vertices of an equilateral triangle whose median is of length 3a is x2+y2=4a2.
View SolutionShow that the isosceles triangle of maximum area that can be inscribed in a given circle is an equilateral triangle .
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf the vertices of a triangle have rational coordinates, then prove that the triangle cannot be equilateral.
View SolutionIf (-4,3) and (4,3) are two vertices of an equilateral triangle, then find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
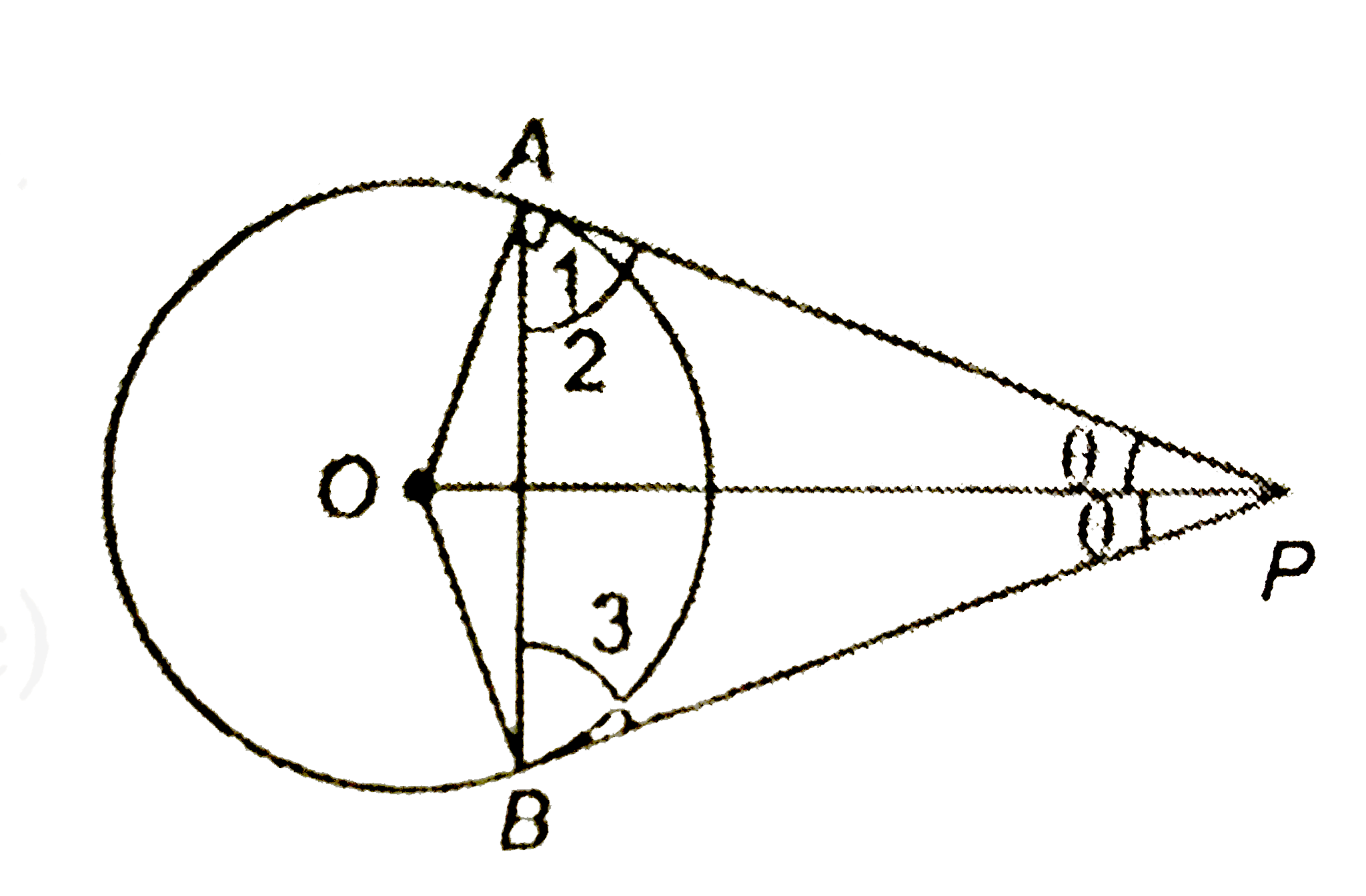
View Solution
