The polar coordinates of the point whose cartesian coordinates are (-1, -1) is
(√2,π4)
(√2,3π4)
(√2,−π4)
(√2,−3π4)
The correct Answer is:D
To find the polar coordinates of the point whose Cartesian coordinates are (-1, -1), we can follow these steps:
Step 1: Identify the Cartesian Coordinates
The given Cartesian coordinates are:
- x = -1
- y = -1
Step 2: Determine the Quadrant
Since both x and y are negative, the point (-1, -1) lies in the third quadrant.
Step 3: Calculate the Radius (R)
The radius R in polar coordinates is calculated using the formula:
R=√x2+y2
Substituting the values:
R=√(−1)2+(−1)2=√1+1=√2
Step 4: Calculate the Angle (θ)
The angle θ can be found using the tangent function:
tan(θ)=yx=−1−1=1
The angle whose tangent is 1 is π4 radians. However, since we are in the third quadrant, we need to add π to this angle:
θ=π+π4=5π4
Step 5: Write the Polar Coordinates
The polar coordinates are given by (R,θ):
Polar Coordinates=(√2,5π4)
Step 6: Check for Equivalent Angles
Since angles can be represented in multiple ways, we can also express 5π4 in a negative direction. This can be done by subtracting 2π:
5π4−2π=5π4−8π4=−3π4
Thus, the angle can also be represented as −3π4.
Final Answer
The polar coordinates of the point (-1, -1) are:
(√2,−3π4)
---
The given Cartesian coordinates are:
- x = -1
- y = -1
Since both x and y are negative, the point (-1, -1) lies in the third quadrant.
The radius R in polar coordinates is calculated using the formula:
R=√x2+y2
Substituting the values:
R=√(−1)2+(−1)2=√1+1=√2
The angle θ can be found using the tangent function:
tan(θ)=yx=−1−1=1
The angle whose tangent is 1 is π4 radians. However, since we are in the third quadrant, we need to add π to this angle:
θ=π+π4=5π4
The polar coordinates are given by (R,θ):
Polar Coordinates=(√2,5π4)
Since angles can be represented in multiple ways, we can also express 5π4 in a negative direction. This can be done by subtracting 2π:
5π4−2π=5π4−8π4=−3π4
Thus, the angle can also be represented as −3π4.
The polar coordinates of the point (-1, -1) are:
(√2,−3π4)
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHS ENGLISHChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise For Session 2
Explore 19 Videos
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHS ENGLISHChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise For Session 3
Explore 19 Videos
- COORDINATE SYSTEM AND COORDINATES Book:ARIHANT MATHS ENGLISHChapter:COORDINATE SYSTEM AND COORDINATES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 7 Videos
- CONTINUITY AND DIFFERENTIABILITYBook:ARIHANT MATHS ENGLISHChapter:CONTINUITY AND DIFFERENTIABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 20 Videos
- DEFINITE INTEGRALBook:ARIHANT MATHS ENGLISHChapter:DEFINITE INTEGRALExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 38 Videos
Similar Questions
Find the polar coordinates of the points whose cartesian coordinates are
(−2,−2)
View SolutionFind the polar coordinates of the points whose cartesian coordinates are
(−3,4)
View SolutionThe cartesian coordinates of the point whose polar coordinates are (13,π−tan−1(512)) is
View SolutionFind the cartesian coordinates of the points whose polar coordinates are
(5,π−tan−1(43))
View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(i) (2,π/3)
(ii) (0.π/2)
(iii) (−√2,π/4)
View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionFind the coor dinates of the centrod of a triangle whose coordinates are (3, -5, 7), (-1, 7, -6)
and (1, 1, 2).
View SolutionConvert the polar coordinates to its equivalent Cartesian coordinates(2,π).
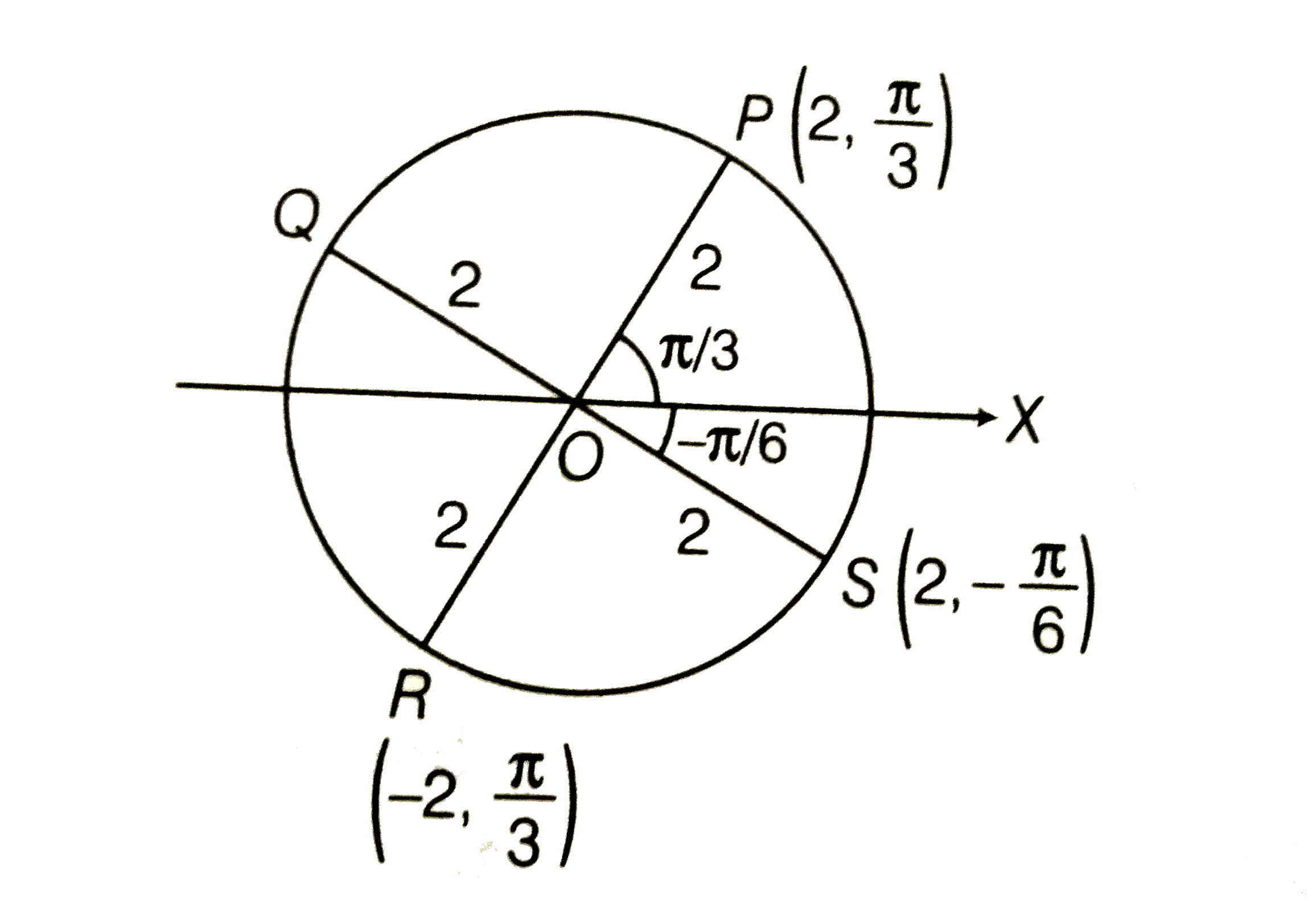
View SolutionThe cartesian coordinates of the point Q in the figure is
View SolutionThe Cartesian coordinates of point having polar coordinates(−2,2π3)will be
View Solution