A straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
The correct Answer is:A, C, D
To find the locus of the midpoint of the line segment AB, where A and B are the points where the line through (1, 1) intersects the x-axis and y-axis respectively, we can follow these steps:
1. Identify Points A and B:
Let the point A be (a, 0) on the x-axis and the point B be (0, b) on the y-axis.
2. Equation of the Line:
The equation of the line passing through the point (1, 1) can be expressed in the intercept form:
xa+yb=1
3. Substituting the Point (1, 1):
Since the line passes through the point (1, 1), we substitute x = 1 and y = 1 into the equation:
1a+1b=1
4. Finding a Relationship Between a and b:
To solve for a and b, we can rearrange the equation:
b+aab=1⟹a+b=ab
5. Midpoint of AB:
The midpoint M of the segment AB can be calculated as:
M=(a+02,0+b2)=(a2,b2)
Let h=a2 and k=b2. Thus, we have:
a=2handb=2k
6. Substituting a and b Back:
Substitute a and b into the equation a+b=ab:
2h+2k=(2h)(2k)
Simplifying gives:
2(h+k)=4hk
7. Final Equation:
Dividing through by 2:
h+k=2hk
Rearranging gives:
h+k−2hk=0
8. Replacing h and k with x and y:
Since h and k represent the coordinates of the midpoint M, we can replace them with x and y:
x+y−2xy=0
Conclusion:
The locus of the midpoint M of the line segment AB is given by the equation:
x+y−2xy=0
Let the point A be (a, 0) on the x-axis and the point B be (0, b) on the y-axis.
The equation of the line passing through the point (1, 1) can be expressed in the intercept form:
xa+yb=1
Since the line passes through the point (1, 1), we substitute x = 1 and y = 1 into the equation:
1a+1b=1
To solve for a and b, we can rearrange the equation:
b+aab=1⟹a+b=ab
The midpoint M of the segment AB can be calculated as:
M=(a+02,0+b2)=(a2,b2)
Let h=a2 and k=b2. Thus, we have:
a=2handb=2k
Substitute a and b into the equation a+b=ab:
2h+2k=(2h)(2k)
Simplifying gives:
2(h+k)=4hk
Dividing through by 2:
h+k=2hk
Rearranging gives:
h+k−2hk=0
Since h and k represent the coordinates of the midpoint M, we can replace them with x and y:
x+y−2xy=0
The locus of the midpoint M of the line segment AB is given by the equation:
x+y−2xy=0
Topper's Solved these Questions
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - Numerical Value Type for JEE Main
15 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - JEE MAIN ARCHIVE
15 Videos
- CONIC SECTIONSBOOK - VMC MODULES ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - LEVEL - 1
178 Videos
- COMPLEX NUMBERS BOOK - VMC MODULES ENGLISHCHAPTER - COMPLEX NUMBERS EXERCISE - JEE ARCHIVE
76 Videos
- DIFFERENTIAL CALCULUSBOOK - VMC MODULES ENGLISHCHAPTER - DIFFERENTIAL CALCULUSEXERCISE - JEE Advanced (Archive)
75 Videos
Similar Questions
A straight line passes through the point P(3, 2). It meets the x-axis at point A and the y-axis at point B. If PAPB=23. find the equation of the line that passes through the point P and is perpendicular to line AB.
View SolutionIf the area (in sq. units) of the triangle formed by the intersection of a line parallel to the x - axis and passing through the point P(h,k) with the line y=x and x+y=2 is 4h2, then the locus of the point P is
View SolutionA line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
View SolutionA straight line passes through the points P(−1,4) and Q(5,−2). It intersects x-axis at point A and y-axis at point B. M is the midpoint of the line segment AB. Find :
the co-ordinates of point M.
View SolutionOA and OB are two perpendicular straight lines. A straight line AB is drawn in such a manner that OA+OB=8. Find the locus of the mid point of AB.
View SolutionIn the figure given below , the line segment AB meets X-axis at A and Y-axis at B. The point P (-3, 4) on AB divides it in the ratio 2:3. Find the coordinates of A and B.
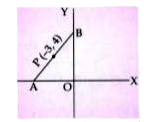
View SolutionA normal to the hyperbola x2−4y2=4 meets the x and y axes at A and B. The locus of the point of intersection of the straight lines drawn through A and B perpendicular to the x and y-axes respectively is
View SolutionA curve C has the property that if the tangent drawn at any point P on C meets the co-ordinate axis at A and B , then P is the mid-point of AB. The curve passes through the point (1,1). Determine the equation of the curve.
View SolutionIf the tangent drawn to the hyperbola 4y2=x2+1 intersect the co-ordinate axes at the distinct points A and B, then the locus of the mid-point of AB is:
View SolutionA variable straight line is drawn through the point of intersection of the straight lines xa+yb=1 and xb+ya=1 and meets the coordinate axes at A and B. Show that the locus of the midpoint of AB is the curve 2xy(a+b)=ab(x+y)
View Solution
