A line segment AB is divided internally and externally in the same ratio at P and Q respectively and M is the mid-point of AB. Statement I : MP, MB, MQ are in G.P. Statement II : AP, AB and AQ are in H.P.
The correct Answer is:A
To solve the problem, we need to analyze the statements given regarding the line segment AB, which is divided internally at point P and externally at point Q in the same ratio, with M as the midpoint of AB.
Step 1: Define the coordinates of points A and B
Let's place point A at the origin (0, 0) and point B at (10, 0).
Step 2: Find the coordinates of point P
Since P divides AB internally in the ratio k:1, we can use the section formula. The coordinates of P can be calculated as:
P=(k⋅xB+1⋅xAk+1,k⋅yB+1⋅yAk+1)
Substituting the coordinates of A and B:
P=(k⋅10+1⋅0k+1,k⋅0+1⋅0k+1)=(10kk+1,0)
Step 3: Find the coordinates of point Q
Point Q divides AB externally in the same ratio k:1. The coordinates of Q can be calculated as:
Q=(k⋅xB−1⋅xAk−1,k⋅yB−1⋅yAk−1)
Substituting the coordinates of A and B:
Q=(k⋅10−1⋅0k−1,k⋅0−1⋅0k−1)=(10kk−1,0)
Step 4: Find the coordinates of midpoint M
The midpoint M of segment AB is given by:
M=(xA+xB2,yA+yB2)=(0+102,0+02)=(5,0)
Step 5: Calculate distances MP, MB, and MQ
Using the distance formula:
- MP=|xP−xM|=∣∣∣10kk+1−5∣∣∣
- MB=|xB−xM|=|10−5|=5
- MQ=|xQ−xM|=∣∣∣10kk−1−5∣∣∣
Step 6: Check if MP, MB, and MQ are in G.P.
For MP, MB, and MQ to be in G.P., the following condition must hold:
MP2=MB⋅MQ
Substituting the distances calculated in Step 5 into this equation will help us determine if they are in G.P.
Step 7: Calculate AP, AB, and AQ
- AP=|xP−xA|=∣∣∣10kk+1−0∣∣∣=10kk+1
- AB=|xB−xA|=|10−0|=10
- AQ=|xQ−xA|=∣∣∣10kk−1−0∣∣∣=10kk−1
Step 8: Check if AP, AB, and AQ are in H.P.
For AP, AB, and AQ to be in H.P., the reciprocals must be in A.P.:
1AP,1AB,1AQ
This means checking if:
1AP−1AB=1AQ−1AP
Conclusion
After performing the calculations, we can conclude whether the statements are true or false based on the conditions derived from the distances.
Let's place point A at the origin (0, 0) and point B at (10, 0).
Since P divides AB internally in the ratio k:1, we can use the section formula. The coordinates of P can be calculated as:
P=(k⋅xB+1⋅xAk+1,k⋅yB+1⋅yAk+1)
Substituting the coordinates of A and B:
P=(k⋅10+1⋅0k+1,k⋅0+1⋅0k+1)=(10kk+1,0)
Point Q divides AB externally in the same ratio k:1. The coordinates of Q can be calculated as:
Q=(k⋅xB−1⋅xAk−1,k⋅yB−1⋅yAk−1)
Substituting the coordinates of A and B:
Q=(k⋅10−1⋅0k−1,k⋅0−1⋅0k−1)=(10kk−1,0)
The midpoint M of segment AB is given by:
M=(xA+xB2,yA+yB2)=(0+102,0+02)=(5,0)
Using the distance formula:
- MP=|xP−xM|=∣∣∣10kk+1−5∣∣∣
- MB=|xB−xM|=|10−5|=5
- MQ=|xQ−xM|=∣∣∣10kk−1−5∣∣∣
For MP, MB, and MQ to be in G.P., the following condition must hold:
MP2=MB⋅MQ
Substituting the distances calculated in Step 5 into this equation will help us determine if they are in G.P.
- AP=|xP−xA|=∣∣∣10kk+1−0∣∣∣=10kk+1
- AB=|xB−xA|=|10−0|=10
- AQ=|xQ−xA|=∣∣∣10kk−1−0∣∣∣=10kk−1
For AP, AB, and AQ to be in H.P., the reciprocals must be in A.P.:
1AP,1AB,1AQ
This means checking if:
1AP−1AB=1AQ−1AP
After performing the calculations, we can conclude whether the statements are true or false based on the conditions derived from the distances.
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - EXERCISE : 7
4 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise (Subjective Type Questions)
5 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - EXERCISE : 5
2 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
A and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the

equation of line AB.
View SolutionA and B are two points on the x-axis and y-axis respectively. P(2, -3) is the mid point of AB. Find the
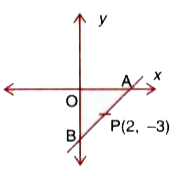
slope of line AB
View SolutionIf the first and the nth term of a G.P. are a and b, respectively, and if P is the product of n terms , prove that P2=(ab)n.
View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
View SolutionIf C and D are the points of internal and external division of line segment AB in the same ratio, then AC,AB, AD are in
View SolutionA line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that : QA = QB.
View SolutionDraw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such
View SolutionIn Figure, AP and BQ are perpendiculars to the line segment AB and AP=BQ . Prove that O is the mid-point of line segment AB and PQ
View SolutionIn the figure, given below, 2AD=AB,P is the mid-point of AB, Q is the mid-point of DR and PR∣∣BS. Prove that :
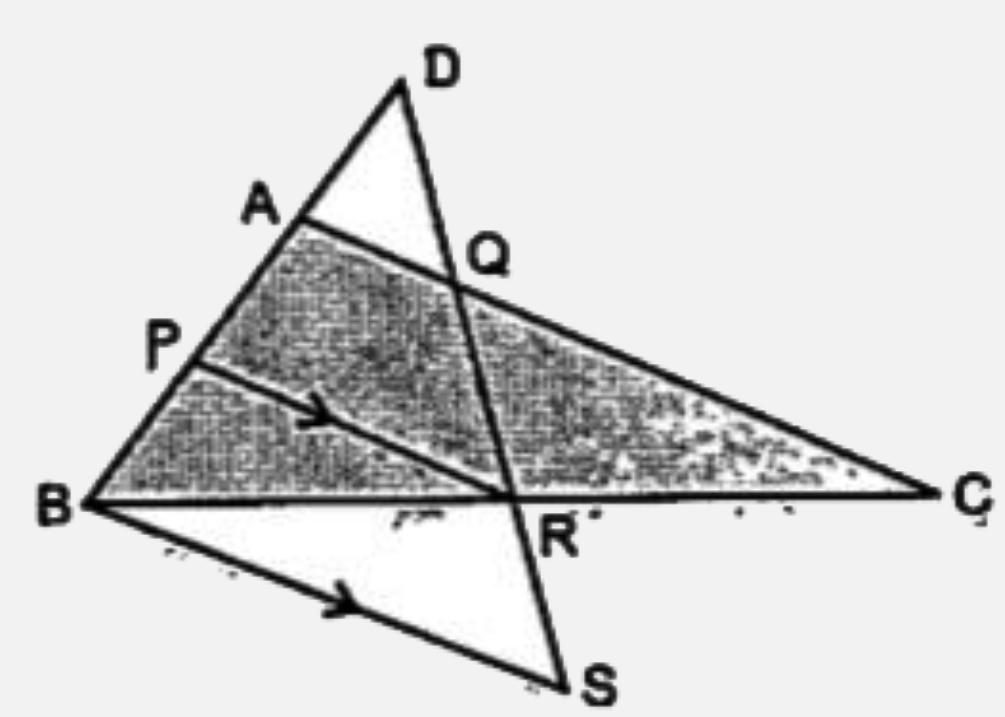
AQ∣∣BS
View SolutionDraw a line segment AB = 6 cm. Take a point P above this line segment. Draw a perpendicular to AB through the point P.
View Solution
