A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
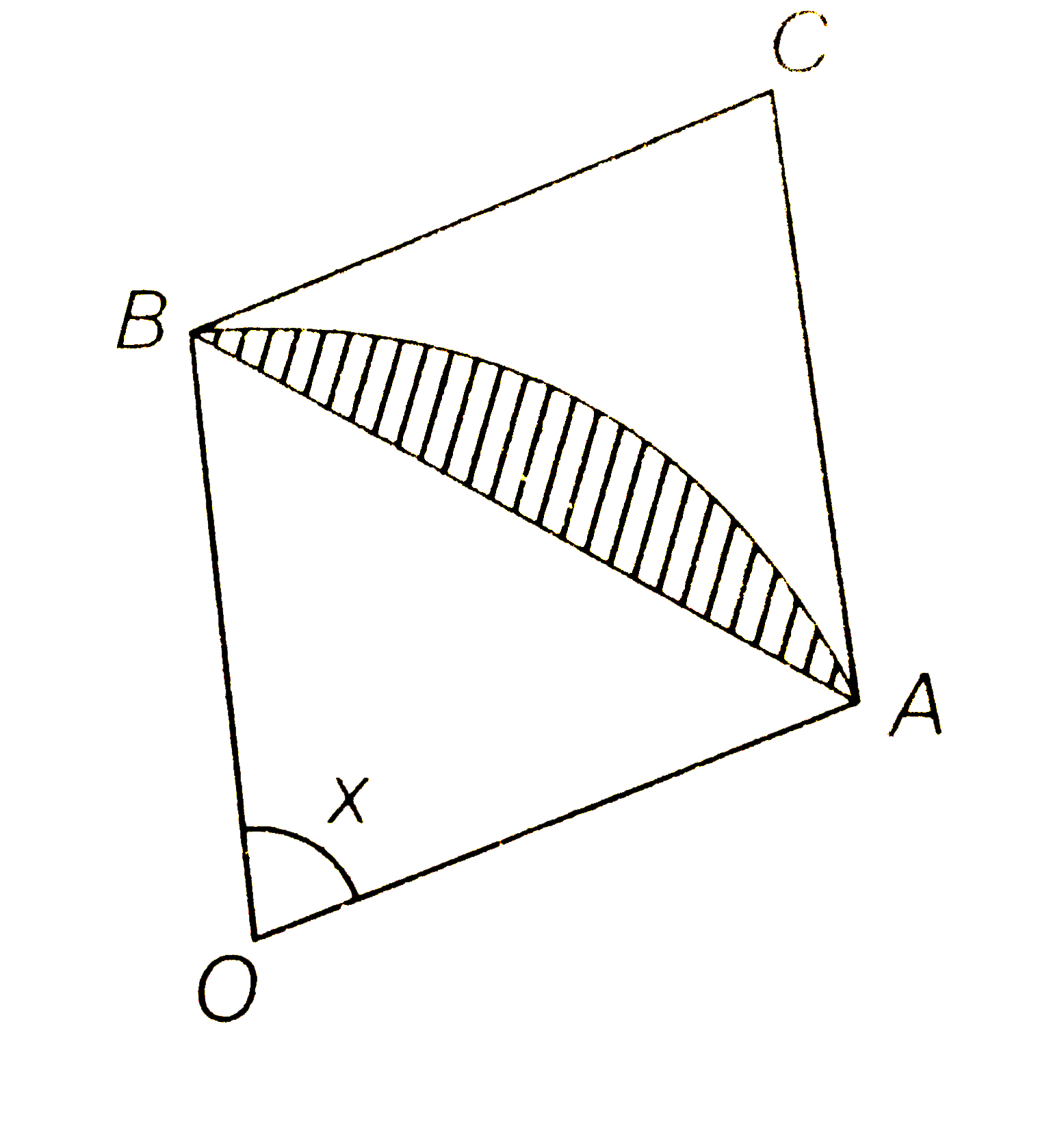
limx→0T(x)x3 is
12
13
14
18
The correct Answer is:D
Step by step video & image solution for A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of DeltaABC and S(x) be the area of shaded region. lim_(xto0)(T(x))/(x^(3)) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (Matching Type Questions)
3 Videos
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - MATCHING TYPE QUESTIONS
1 Videos
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
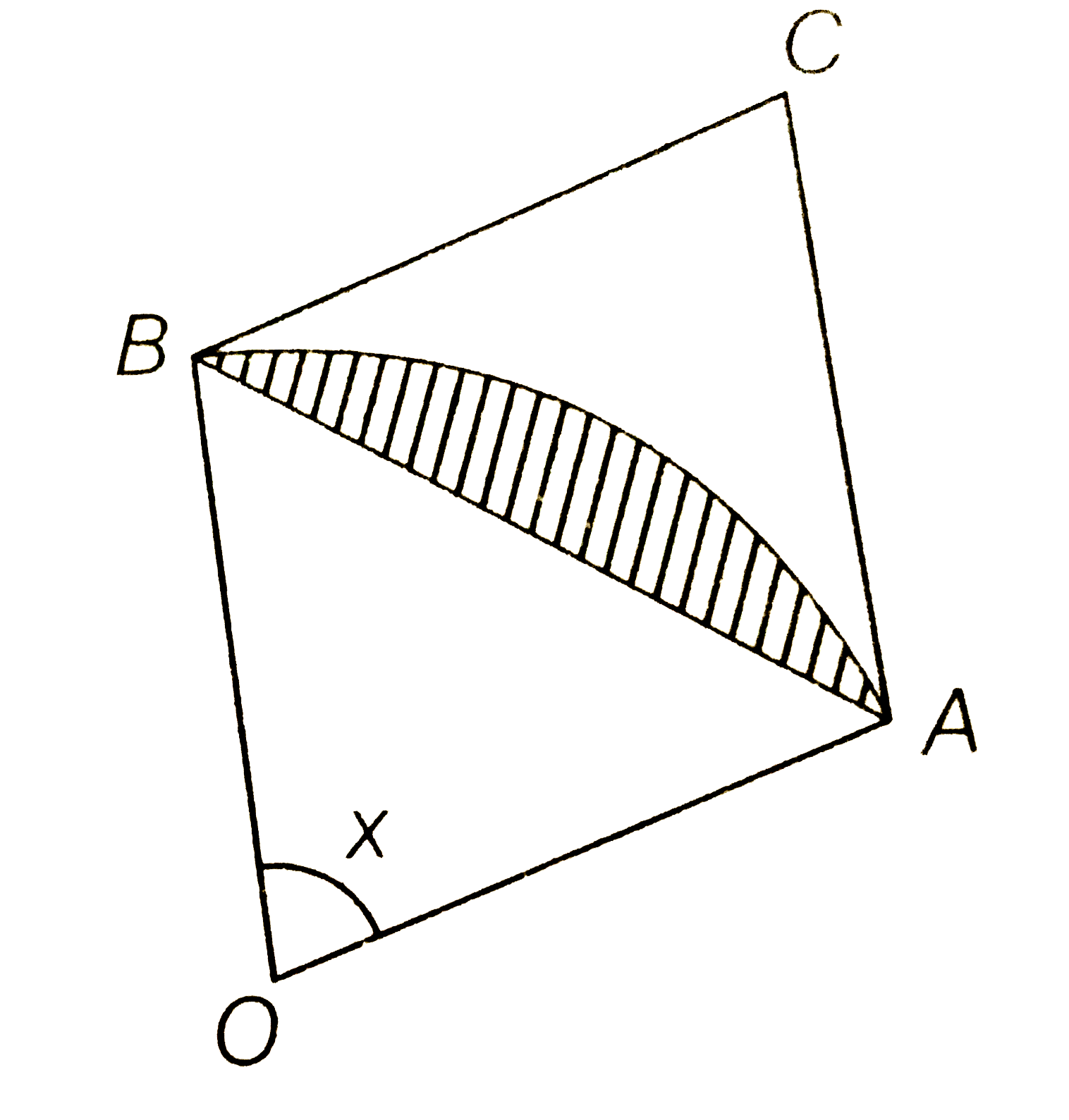
limx→0S(x)x is
View SolutionA circular are of radius 1 subtends an angle of x radians 0<x<π2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x)&S(x)&limx→0T(x)S(x)
View SolutionAn arc AB of a circle subtends an angle x radians at the center O of the circle. Given that the area of the sector AOB is equal to the square of the length of the arc AB, find the value of x.
View SolutionEquation of the tangent to the circle at the point (1, -1) whose centre is the point of intersection of the straight lines x-y=1 and 2x+y-3=0, is
View SolutionIn a circle of radius 21cm, an arc subtends an angle of 600 at the centre. Find (i) the length of the arc (ii) area of the sector formed by the arc. (Useπ227)
View SolutionIn a circle of radius 21cm, an arc subtends an angle of 600 at the centre. Find (i) the length of the arc (ii) area of the sector formed by the arc. (Useπ227)
View SolutionThe straight line x-2y+1=0 intersects the circle x2+y2=25 in points P and Q the coordinates of the point of intersection of tangents drawn at P and Q to the circle is
View SolutionFind the values of a and b in order that
limx→0x(1+acosx)−bsinxx3=1.
View SolutionThe equation of the circle having centre (0, 0) and passing through the point of intersection of the lines 4x+3y=2andx+2y=3 is
View SolutionAB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB=30∘ , find the area of the shaded region.
View Solution
