A circular are of radius 1 subtends an angle of x radians 0<x<π2 as shown in the figure . the point r is the intersection of the two tangent line at P and Q. let T(x) be the area of triangle PQR and S(x) be the area of the shaded region then find T(x)&S(x)&limx→0T(x)S(x)
14
34
32
0
The correct Answer is:C
To solve the problem, we need to find the areas T(x) and S(x), and then compute the limit limx→0T(x)S(x).
Step 1: Finding T(x) (Area of Triangle PQR)
1. Identify the triangle: Triangle PQR is formed by points P, Q, and R where P and Q are points on the circle of radius 1, and R is the intersection of the tangents at P and Q.
2. Use tangent properties: The angle subtended at the center by the arc PQ is x radians. The angles at R (formed by tangents) are x2 each.
3. Length of tangents: Let l be the length of the tangent from point R to points P and Q. Using the tangent property in triangle PRO (where O is the center of the circle):
tan(x2)=l1⟹l=tan(x2)
4. Area of triangle formula: The area T(x) of triangle PQR can be calculated using the formula:
T(x)=12×base×height=12×PQ×h
where PQ=2sin(x2) and h=l=tan(x2).
5. Calculate T(x):
T(x)=12×2sin(x2)×tan(x2)=sin(x2)tan(x2)
Step 2: Finding S(x) (Area of the Shaded Region)
1. Area of the sector: The area of the sector OPQ is given by:
Area of sector=12r2θ=12⋅12⋅x=x2
2. Area of triangle POQ: The area of triangle POQ can be calculated as:
Area of triangle=12⋅r2⋅sin(x)=12⋅12⋅sin(x)=sin(x)2
3. Calculate S(x):
S(x)=Area of sector−Area of triangle=x2−sin(x)2
Step 3: Finding the Limit limx→0T(x)S(x)
1. Substituting T(x) and S(x):
limx→0T(x)S(x)=limx→0sin(x2)tan(x2)x2−sin(x)2
2. Simplifying the denominator:
x2−sin(x)2=x−sin(x)2
3. Using L'Hôpital's Rule: Since both the numerator and denominator approach 0 as x→0:
limx→0sin(x2)tan(x2)x−sin(x)2=limx→02sin(x2)tan(x2)x−sin(x)
4. Differentiating: Differentiate the numerator and denominator separately and evaluate the limit.
Final Result
After performing the necessary calculations, we find:
limx→0T(x)S(x)=3
2. Use tangent properties: The angle subtended at the center by the arc PQ is x radians. The angles at R (formed by tangents) are x2 each.
3. Length of tangents: Let l be the length of the tangent from point R to points P and Q. Using the tangent property in triangle PRO (where O is the center of the circle):
tan(x2)=l1⟹l=tan(x2)
4. Area of triangle formula: The area T(x) of triangle PQR can be calculated using the formula:
T(x)=12×base×height=12×PQ×h
where PQ=2sin(x2) and h=l=tan(x2).
5. Calculate T(x):
T(x)=12×2sin(x2)×tan(x2)=sin(x2)tan(x2)
Area of sector=12r2θ=12⋅12⋅x=x2
2. Area of triangle POQ: The area of triangle POQ can be calculated as:
Area of triangle=12⋅r2⋅sin(x)=12⋅12⋅sin(x)=sin(x)2
3. Calculate S(x):
S(x)=Area of sector−Area of triangle=x2−sin(x)2
limx→0T(x)S(x)=limx→0sin(x2)tan(x2)x2−sin(x)2
2. Simplifying the denominator:
x2−sin(x)2=x−sin(x)2
3. Using L'Hôpital's Rule: Since both the numerator and denominator approach 0 as x→0:
limx→0sin(x2)tan(x2)x−sin(x)2=limx→02sin(x2)tan(x2)x−sin(x)
4. Differentiating: Differentiate the numerator and denominator separately and evaluate the limit.
limx→0T(x)S(x)=3
Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (Matching Type Questions)
3 Videos
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - MATCHING TYPE QUESTIONS
1 Videos
- LIMITSBOOK - ARIHANT MATHS ENGLISHCHAPTER - LIMITSEXERCISE - Exercise (More Than One Correct Option Type Questions)
15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
2 Videos
Similar Questions
A circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
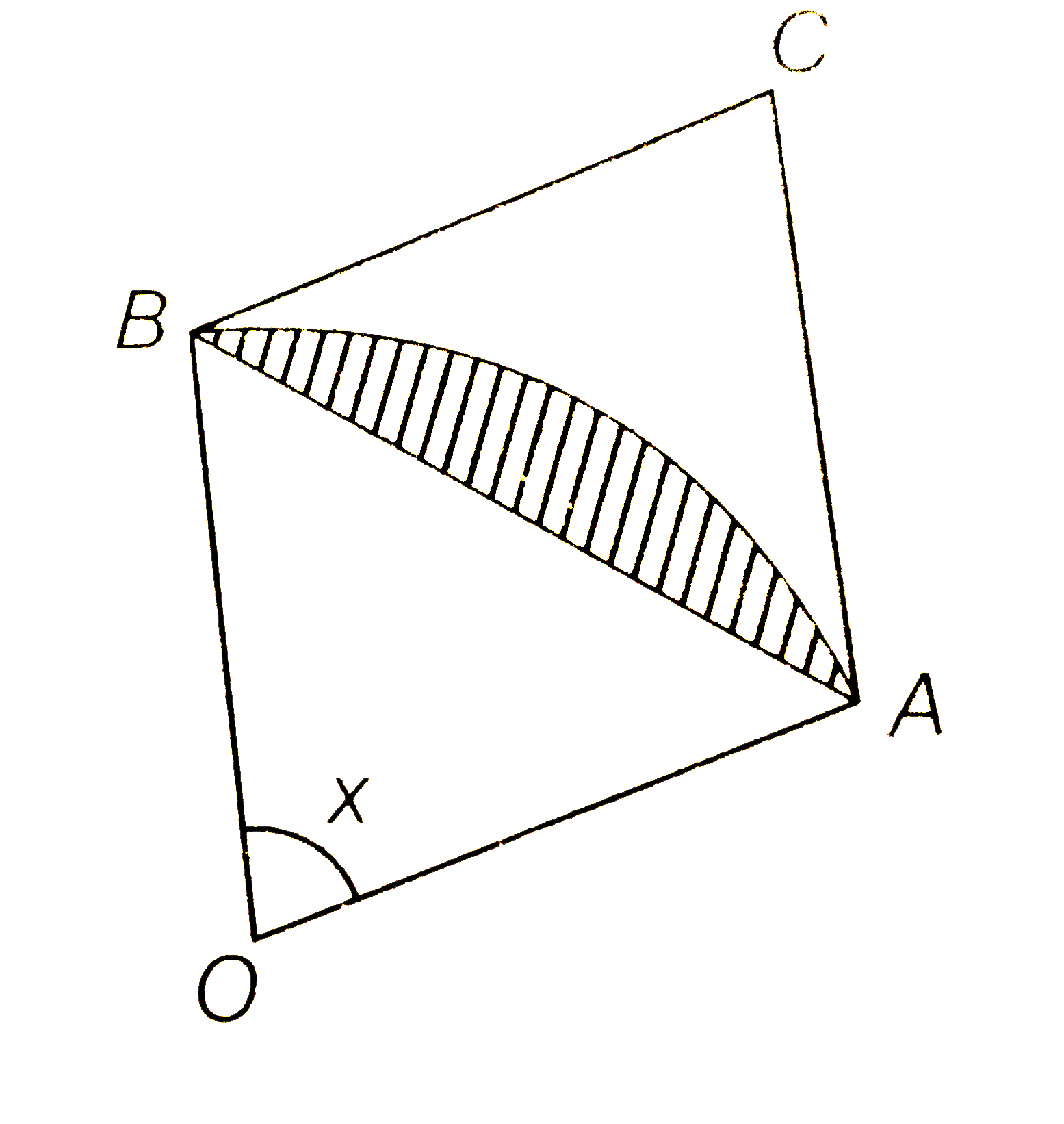
limx→0T(x)x3 is
View SolutionA circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let T(x) be the area of ΔABC and S(x) be the area of shaded region.
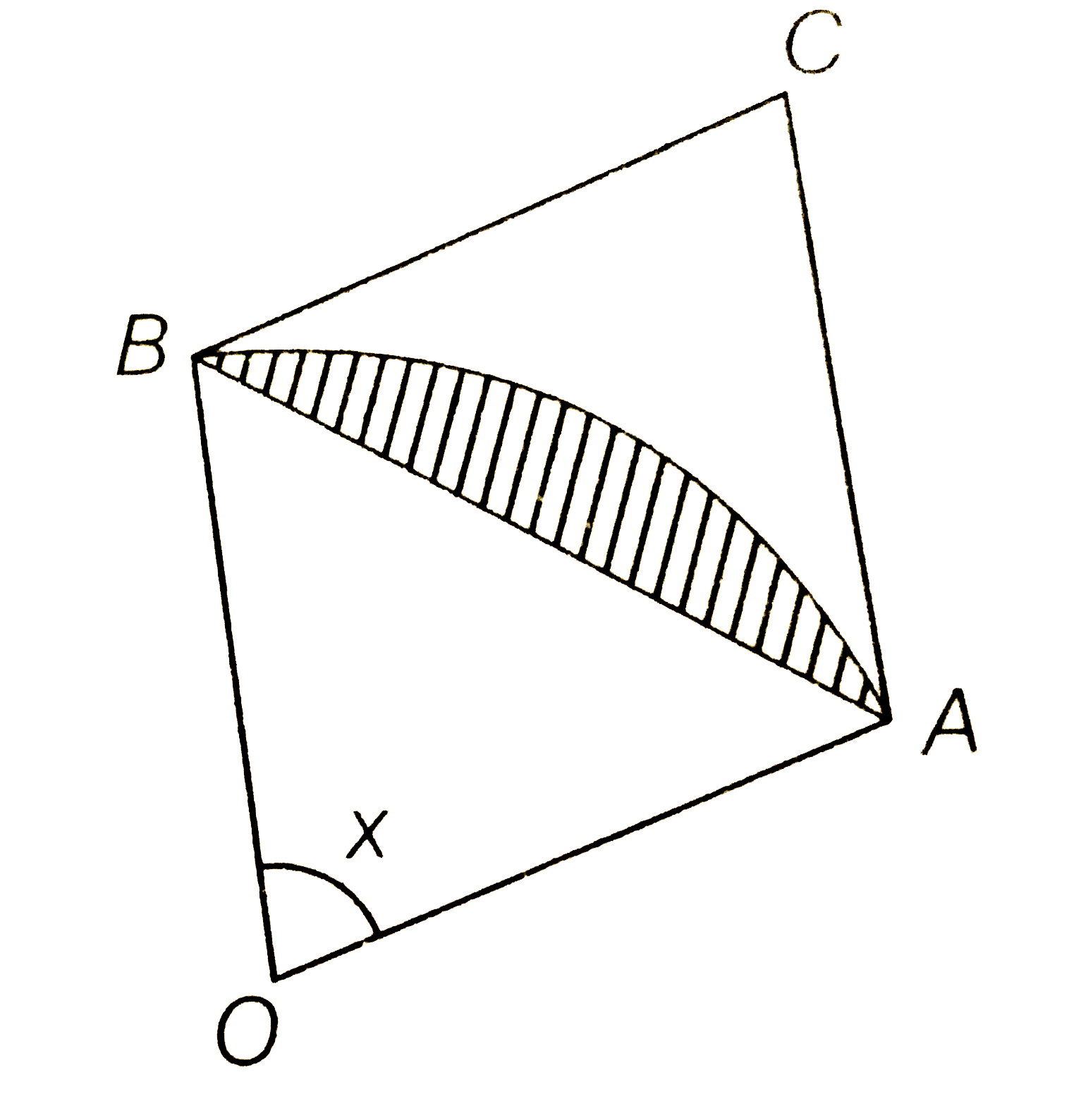
limx→0S(x)x is
View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View SolutionAn arc AB of a circle subtends an angle x radians at the center O of the circle. Given that the area of the sector AOB is equal to the square of the length of the arc AB, find the value of x.
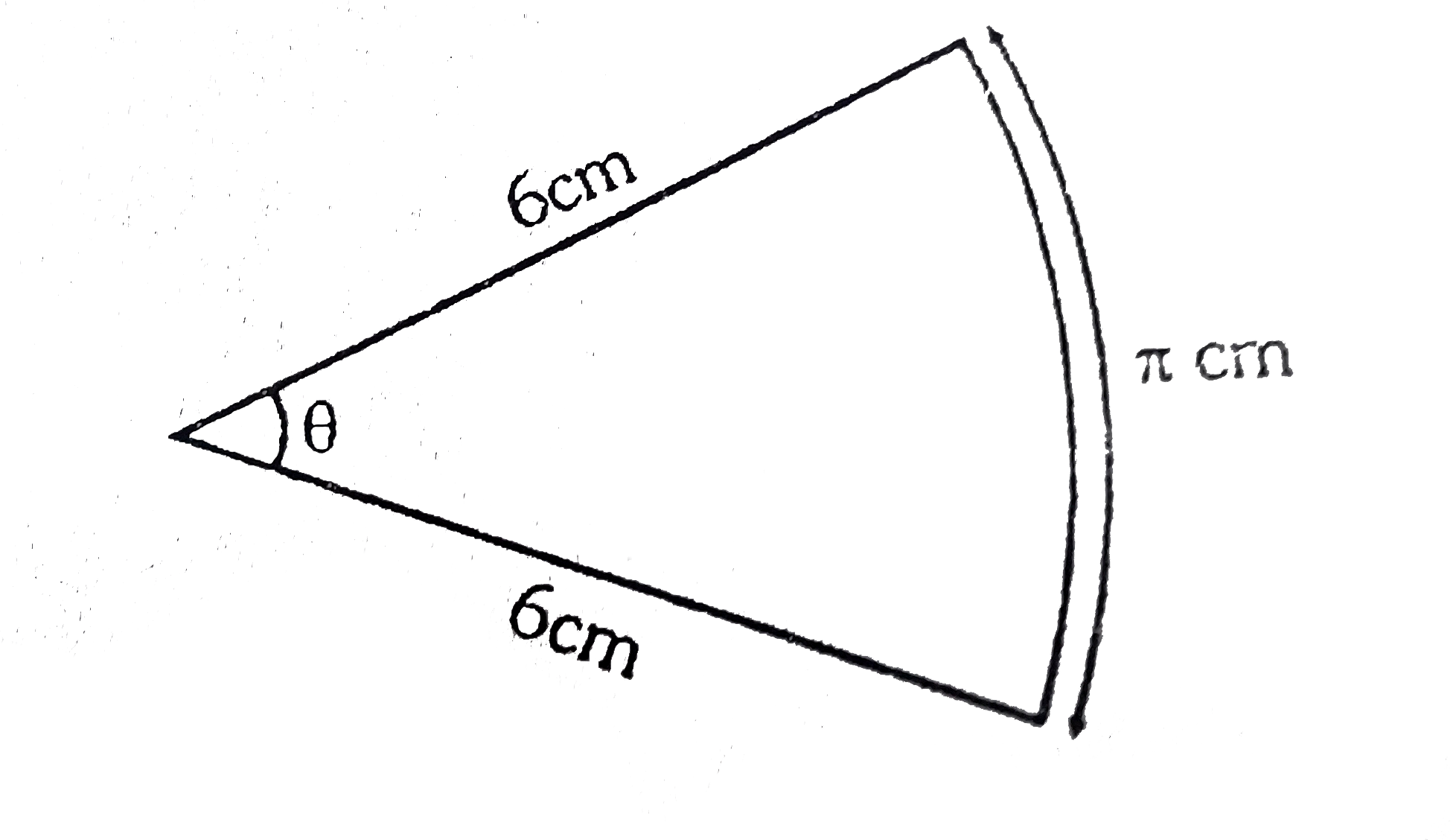
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
View SolutionShow that f(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩sin3xtan2xifx<032ifx=0log(1+3x)e2x−1ifx>0 is continuous at x=0
View SolutionIf the chord y=mx+1 of the circles x2+y2=1 subtends an angle of 450 at the major segment of the circle, then the value of m is 2 (b) −2 (c) +1 (d) none of these
View SolutionThe value of (lim)x→π/2(secx−tanx) is a. 1 b . 0 c. 2 d. -1
View SolutionEnergy of a satellite in circular orbit is E0. The energy required to move the satellite to a circular orbit of 3 time the radius of the initial orbit is x3E0. Find the value of x.
View Solution
