Differentiate |x|+a0xn+a1xn−1+a2xn−1+...+an−1x+an
The correct Answer is:x|x|+na0xn−1+(n−1)a1xn−2+(n−2)a2xn−3+...+an−11
To differentiate the function y=|x|+a0xn+a1xn−1+a2xn−2+…+an−1x+an, we can break it down into two parts: y1=|x| and y2=a0xn+a1xn−1+a2xn−2+…+an−1x+an.
Step 1: Differentiate y1=|x|
The absolute value function can be expressed as:
|x|={xif x≥0−xif x<0
Thus, the derivative of |x| is:
ddx|x|=⎧⎨⎩1if x>0−1if x<0undefinedif x=0
Step 2: Differentiate y2
Now, we differentiate y2:
y2=a0xn+a1xn−1+a2xn−2+…+an−1x+an
Using the power rule for differentiation, we have:
dy2dx=a0⋅nxn−1+a1⋅(n−1)xn−2+a2⋅(n−2)xn−3+…+an−1
The constant term an differentiates to zero.
Step 3: Combine the derivatives
Now, we combine the derivatives of y1 and y2:
dydx=dy1dx+dy2dx
Thus, we have:
dydx=⎧⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪⎩1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x>0−1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x<0undefinedif x=0
Final Answer
The derivative of the function y=|x|+a0xn+a1xn−1+a2xn−2+…+an−1x+an is:
dydx=⎧⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪⎩1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x>0−1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x<0undefinedif x=0
|x|={xif x≥0−xif x<0
ddx|x|=⎧⎨⎩1if x>0−1if x<0undefinedif x=0
y2=a0xn+a1xn−1+a2xn−2+…+an−1x+an
dy2dx=a0⋅nxn−1+a1⋅(n−1)xn−2+a2⋅(n−2)xn−3+…+an−1
dydx=dy1dx+dy2dx
dydx=⎧⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪⎩1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x>0−1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x<0undefinedif x=0
dydx=⎧⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪⎩1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x>0−1+(a0nxn−1+a1(n−1)xn−2+a2(n−2)xn−3+…+an−1)if x<0undefinedif x=0
Topper's Solved these Questions
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 2
27 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 3
9 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- DIFFERENTIAL EQUATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIAL EQUATION EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
26 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
Similar Questions
Differentiate the following with respect of x:a0xn+a1xn−1+a2xn−2++an−1x+an.
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
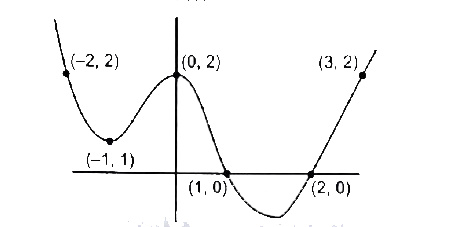
The product of all imaginary roots of p(x)=0 is:
View SolutionIf a1,a2,a3,a4,,……,an−1,an are distinct non-zero real numbers such that (a21+a22+a23+…..+a2n−1)x2+2(a1a2+a2a3+a3a4+……+an−1an)x+(a22+a23+a24+......+a2n)≤0 then a1,a2,a3,.....,an−1,an are in
View SolutionIf a0,a1,a2,… are the coefficients in the expansion of
(1+x+x2)n in ascending powers of x, prove that
a0a2−a1a3+a2a4−…+a2n−2a2n=an+1 .
View SolutionIf (x+a1)(x+a2)(x+a3)…(x+an)=xn+S1xn−1+S2xn−2+…+Sn
where ,S1=n∑i=0ai,S2=(∑∑)1≤i<j≤naiaj,S3(∑∑∑)1≤i<k≤naiajak
and so on .
Coefficient of x7 in the expansion of
(1+x)2(3+x)3(5+x)4 is
View SolutionIf (x+a1)(x+a2)(x+a3)…(x+an)=xn+S1xn−1+S2xn−2+…+Sn
where , S1=n∑i=0ai,S2=(∑∑)1≤i<j≤naiaj,S3(∑∑∑)1≤i<k≤naiajak
and so on .
If (1+x)n=C0+C1x+C2x2+...+Cnxn the
cefficient of xn in the expansion of
(x+C0)(x+C1)(x+C2)...(x+Cn) is
View SolutionIf the equation anxn+an−1xn−1+..+a1x=0,a1≠0,n≥2, has a positive root x=α then the equation nanxn−1+(n−1)an−1xn−2+….+a1=0 has a positive root which is
View SolutionIf (1+x+x2+x3)n=a0+a1x+a2x2+a3x3+...+a3nx3n, then the
value of a0+a4+a8+a12+….. is
View SolutionIf a1,a2,a3,...,an are non-zero real numbers such that
(a21+a22+...+an−1.2)(a22+a23+...+a2n)≤(a1a2+a2a3+...+an−1an)2 then,a1,a2,....an are in
View SolutionIf the sequence a1,a2,a3,…,an is an A.P., then prove that a21−a22+a23−a24+…+a22n−1−a22n=n2n−1(a21−a22n)
View Solution
