Consider the curve f(x)=x13, then
the equation of tangent at (0, 0) is x = 0
the equation of normal at (0, 0) is y = 0
normal to the curve does not exist at (0, 0)
f(x) and its inverse meet at exactly 3 points
The correct Answer is:A, B, D
To solve the problem, we will analyze the curve given by the function f(x)=x1/3 and find the equations of the tangent and normal at the point (0,0). We will also check the validity of the statements provided in the question.
1. Find the derivative f′(x):
f(x)=x1/3
Using the power rule:
f′(x)=13x−23=13√(3)x2
2. Evaluate the derivative at the point (0,0):
f′(0)=13√(3)02 is undefined (infinite)
This indicates that the slope of the tangent line at this point is vertical.
3. Equation of the tangent line:
Since the slope is infinite, the equation of the tangent line at (0,0) is:
x=0
4. Find the slope of the normal line:
The slope of the normal line is the negative reciprocal of the slope of the tangent. Since the slope of the tangent is infinite, the slope of the normal is:
mn=0
5. Equation of the normal line:
Using the point-slope form of the line equation:
y−0=0⋅(x−0)⟹y=0
6. Check the validity of the options:
- Option 1: The equation of the tangent at (0,0) is x=0 (Correct).
- Option 2: The equation of the normal at (0,0) is y=0 (Correct).
- Option 3: The normal to the curve does not exist at (0,0) (Incorrect, as we found y=0).
- Option 4: f(x) and its inverse meet at exactly three points. The inverse function f−1(x)=x3. Setting f(x)=f−1(x):
x1/3=x3⟹x9=x⟹x(x8−1)=0
This gives us x=0 and x=1,−1 (three solutions). Thus, this option is also correct.
Final Conclusion:
- The equations of the tangent and normal at the point (0,0) are x=0 and y=0 respectively.
- The statements regarding the tangent and normal are correct except for the one stating that the normal does not exist.
f(x)=x1/3
Using the power rule:
f′(x)=13x−23=13√(3)x2
f′(0)=13√(3)02 is undefined (infinite)
This indicates that the slope of the tangent line at this point is vertical.
Since the slope is infinite, the equation of the tangent line at (0,0) is:
x=0
The slope of the normal line is the negative reciprocal of the slope of the tangent. Since the slope of the tangent is infinite, the slope of the normal is:
mn=0
Using the point-slope form of the line equation:
y−0=0⋅(x−0)⟹y=0
- Option 1: The equation of the tangent at (0,0) is x=0 (Correct).
- Option 2: The equation of the normal at (0,0) is y=0 (Correct).
- Option 3: The normal to the curve does not exist at (0,0) (Incorrect, as we found y=0).
- Option 4: f(x) and its inverse meet at exactly three points. The inverse function f−1(x)=x3. Setting f(x)=f−1(x):
x1/3=x3⟹x9=x⟹x(x8−1)=0
This gives us x=0 and x=1,−1 (three solutions). Thus, this option is also correct.
- The equations of the tangent and normal at the point (0,0) are x=0 and y=0 respectively.
- The statements regarding the tangent and normal are correct except for the one stating that the normal does not exist.
Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Passage Based Questions)
8 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Single Option Correct Type Questions)
34 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
If the area bounded by the curve f(x)=x13(x−1) and the x-axis is A, then the value of 28A is____
View SolutionIf the area bounded by the curve f(x)=x1/3(x−1) and the x-axis is A, then the value of 28A is__.
View SolutionConsider the cubic equation f(x)=x3−nx+1=0 where n≥3,n∈N then f(x)=0 has
View SolutionCalculate the area enclosed under the curve f(x)=x2 between the limits x=2 and x=3 (figure)
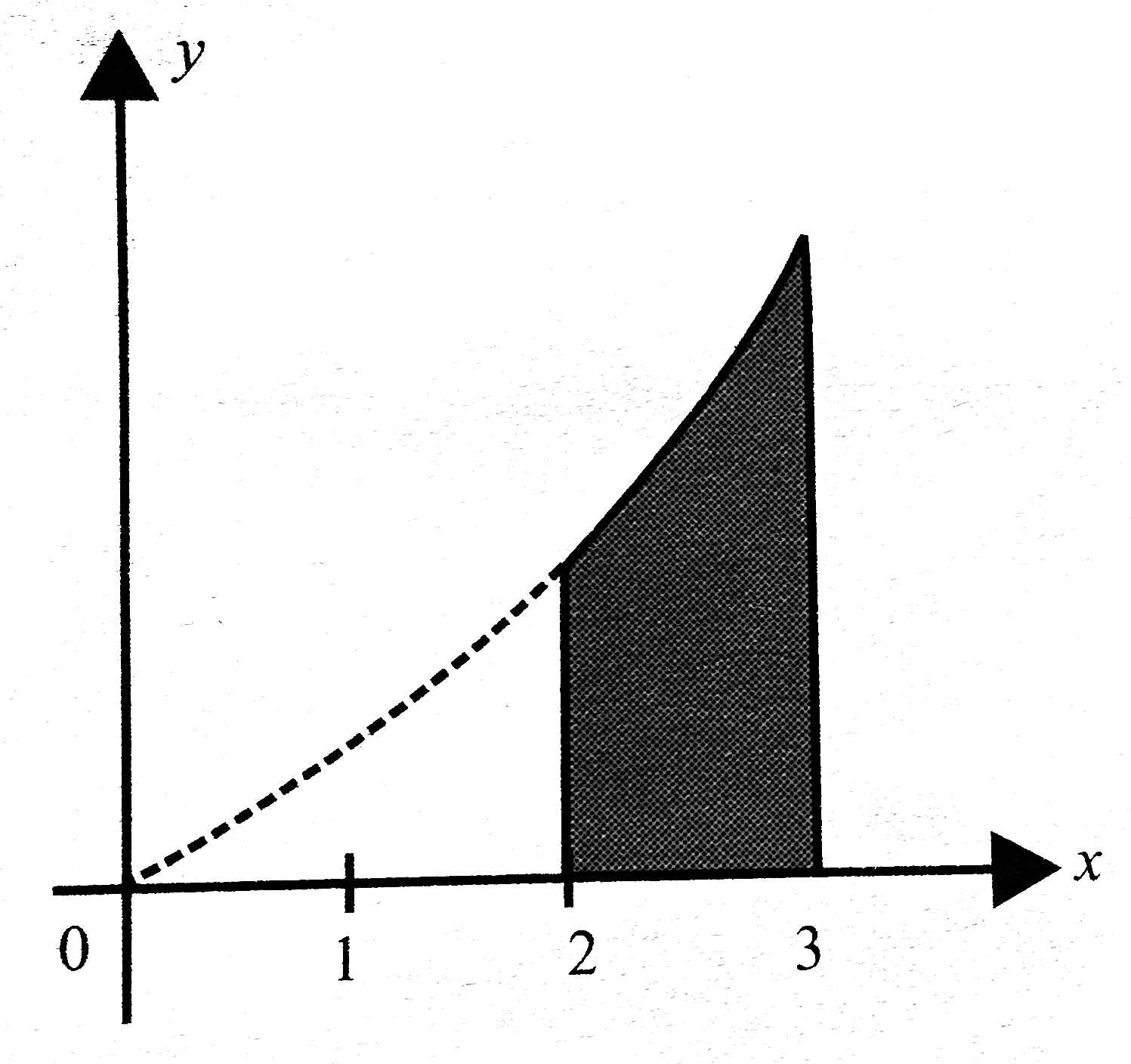
View SolutionConsider the function f(x)=∣∣x3+1∣∣. Then,
View SolutionConsider the function f(x)={2x+3,x≤1and−x2+6,x>1} Then draw the graph of the function y=f(x),y=f(|x|)andy=|f(x)|.
View SolutionThe area (in sq. units) bounded by the curve f(x)=max(|x|−1,1−|x|) with the x- axis from x=−1 to x=1 is
View SolutionConsider the function f(x)=(x3−x)∣∣x2−6x+5∣∣,∀x∈R, then f(x) is
View SolutionConsider the function f(x)={2x+3,x≤1−x2+6,x>1
View SolutionConsider the function f(x) = 2x + 3 and we want to find the limit of this function at x = 1.
View Solution
