For function f(x)=lnxx, which of the following statements are true?
(a)f(x) has horizontal tangent at x = e
(b)f(x) cuts the X-axis only at one point
(c)f(x) is many-one function
(d)f(x) has one vertical tangent
The correct Answer is:A, B, C
To analyze the function f(x)=lnxx and determine which statements are true, we will go through each option step by step.
Step 1: Find the derivative of f(x)
To find the horizontal tangent, we first need to differentiate f(x):
f′(x)=ddx(lnxx)
Using the quotient rule, where u=lnx and v=x:
f′(x)=v⋅u′−u⋅v′v2
Calculating u′ and v′:
- u′=1x
- v′=1
Substituting these into the quotient rule gives:
f′(x)=x⋅1x−lnx⋅1x2=1−lnxx2
Step 2: Determine where f′(x)=0
To find the points where the function has horizontal tangents, we set f′(x)=0:
1−lnxx2=0
This implies:
1−lnx=0⟹lnx=1⟹x=e
Conclusion for Option A: f(x) has a horizontal tangent at x=e (True).
Step 3: Find where f(x) cuts the x-axis
To find where f(x) cuts the x-axis, we set f(x)=0:
lnxx=0
This implies:
lnx=0⟹x=1
Conclusion for Option B: f(x) cuts the x-axis only at one point, x=1 (True).
Step 4: Determine if f(x) is a many-to-one function
To analyze the monotonicity of f(x), we check the sign of f′(x):
- For x<e: lnx<1 implies f′(x)>0 (increasing).
- For x>e: lnx>1 implies f′(x)<0 (decreasing).
Since f(x) is increasing on (0,e) and decreasing on (e,∞), it is not one-to-one. Thus, it is a many-to-one function.
Conclusion for Option C: f(x) is a many-to-one function (True).
Step 5: Check for vertical tangents
Vertical tangents occur where f′(x) is undefined or approaches infinity. Since f′(x)=1−lnxx2, we check where the denominator is zero:
x2=0⟹x=0
However, x=0 is not in the domain of f(x) (since lnx is undefined for x≤0). Therefore, there are no vertical tangents.
Conclusion for Option D: f(x) does not have a vertical tangent (False).
Final Summary of Statements:
- A: True
- B: True
- C: True
- D: False
- v′=1
- For x>e: lnx>1 implies f′(x)<0 (decreasing).
- A: True
- B: True
- C: True
- D: False
Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Passage Based Questions)
8 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Single Option Correct Type Questions)
34 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
Knowledge Check
If g(x)=(x−2)2−5, which of the following statements is true ?
AThe function g (x) is increasing over the entire domain.BThe functin g (x) is decreasing over the entire domain.CThe function g (x) is increasing for x<2 and decreasing for x>2.DThe function g (x) is decreasing for x<2 and increasing for x>2.If f(x)=x3, which of the following must be true ?
Af(−x)=f(x)Bf(−x)=−f(−x)Cf(−x)=−f(x)Df(x)=−f(x)
Let f(x)=cos−1⎛⎜⎝1−tan2(x)21+tan2(x)2⎞⎟⎠. Then which of the following statement is/are true ?
View SolutionLet a function f(x) be definded by f(x)=x−|x−1|x
which of the following is not true ?
View SolutionLet f be a real valued function such that for any real x f(15+x)=f(15−x)andf(30+x)=−f(30−x)
Then which of the following statements is true ?
View SolutionLet f(x)=sinx,g(x)=cosx, then which of the following statement is false period of f(g(x)) is 2π period of f(g(x)) is π f(g(x)) is an odd function f(g(x)) is an even function
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
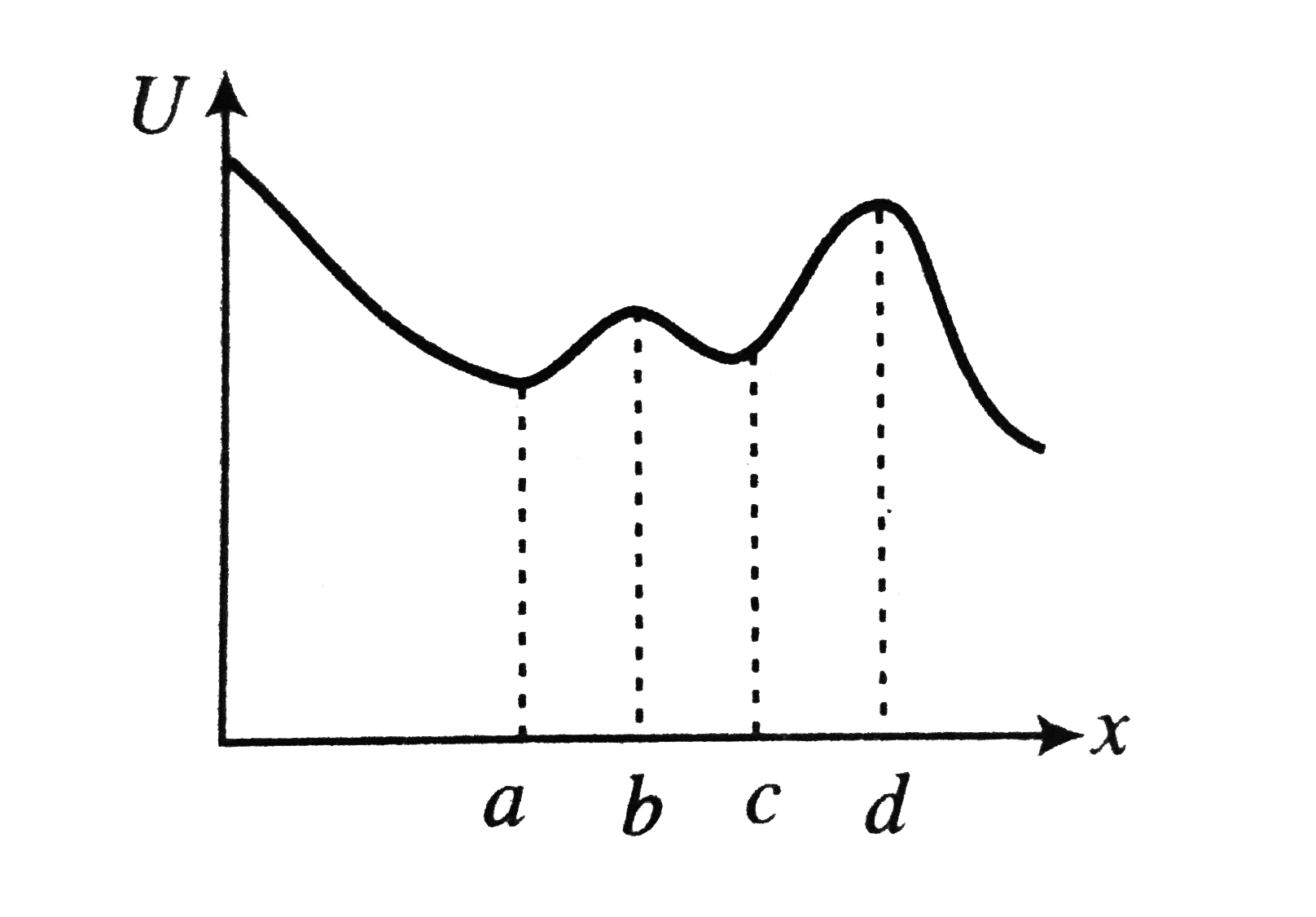
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?

View Solution
