Statements I Tangents at two distinct points of a cubic polynomial cannot coincide.
Statement II If p(x) is a polynomial of degree n(n≥2), then p'(x)+k cannot hold for n or more distinct values of x.
Statement I is true, Statement II is also true, Statement II is the correct explanation of Statement I.
Statement I is true, Statement II is also true, Statement II is not the correct explanation of Statement I
Statement I is true, Statement II is false
Statement I is false, Statement II is true
The correct Answer is:D
Step by step video & image solution for Statements I Tangents at two distinct points of a cubic polynomial cannot coincide. Statement II If p(x) is a polynomial of degree n(nge2), then p'(x)+k cannot hold for n or more distinct values of x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHS ENGLISHChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (Passage Based Questions)
Explore 8 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHS ENGLISHChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:EXERCISE : 5
Explore 1 Video
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Book:ARIHANT MATHS ENGLISHChapter:DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS Exercise:Exercise (More Than One Correct Option Type Questions)
Explore 15 Videos
- DIFFERENTIATION Book:ARIHANT MATHS ENGLISHChapter:DIFFERENTIATION Exercise:Exercise For Session 10
Explore 4 Videos
- ELLIPSEBook:ARIHANT MATHS ENGLISHChapter:ELLIPSEExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 27 Videos
Similar Questions
Knowledge Check
If p(x) is a polynomial function and p(4)=0, then which statement is true?
Ax+4 is a factor of p(x)Bx-4 is a factor of p(x)CThe greatest power of x in p(x) is 4.Dp(x) is divisible by 4.If p(x) is a polynomial function and p(-1)=3, which statement is true?
AThe remainder when p(x) is divided by x-3 is -1.BThe remainder when p(x) is divided by x+3 is -1.CThe remainder when p(x) is divided by x-1 is 3.DThe remainder when p(x) is divided by x+1 by 3.If p(x) is a polynomial function with p(3)=0, which statement must be true?
Ap(x) is divisible by 3.Bx-3 is factor of p(x)Cp(x) is divisible by x+3DThe highest power of x in p(x) is 3.
If P(x) is polynomial of degree 4 such than P(−1)=P(1)=5andP(−2)=P(0)=P(2)=2 find the maximum vaue of P (x).
View SolutionLet P(x) be a polynomial of degree 11 such that P(x)=1x+1 for x=0,1,2,3,….11. The value of P(12) is.
View SolutionStatement 1: The point of intersection of the tangents at three distinct points A,B,andC on the parabola y2=4x can be collinear. Statement 2: If a line L does not intersect the parabola y2=4x, then from every point of the line, two tangents can be drawn to the parabola.
View SolutionIf f(x) is a polynomial of degree n(>2) and f(x)=f(α−x),
(where α is a fixed real number ), then the degree of f'(x) is
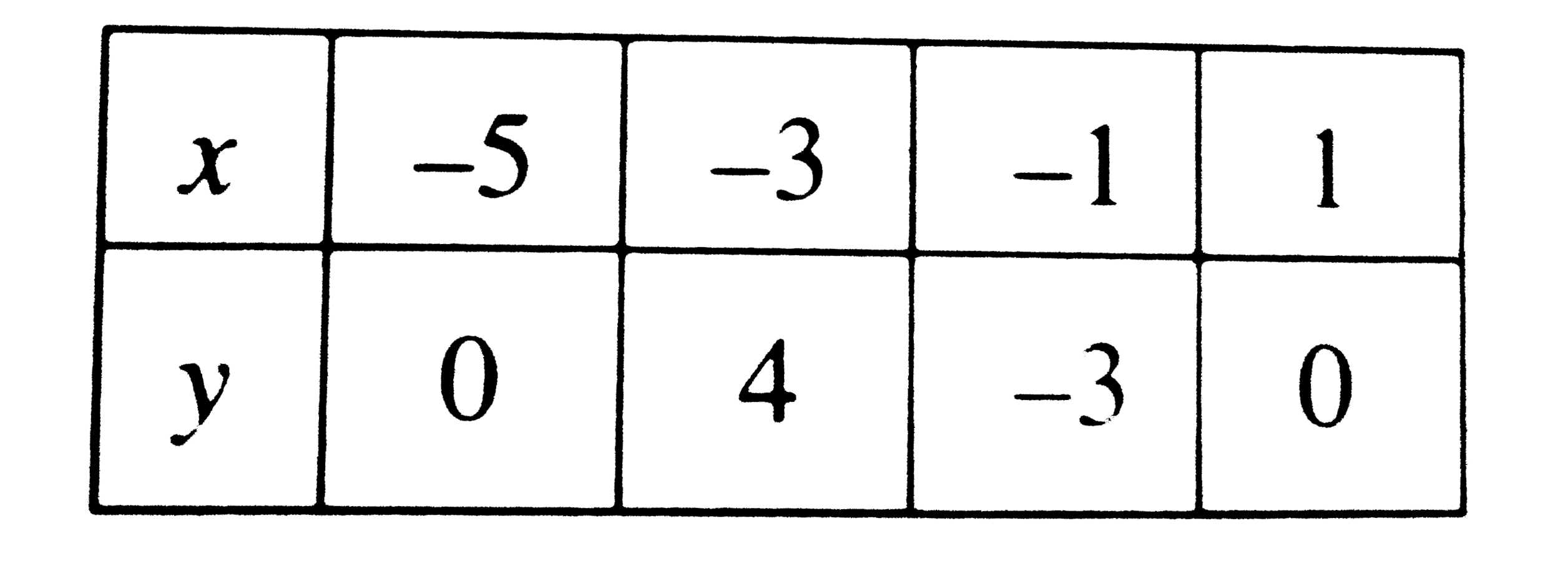
View Solutionx−5−3−11y04−30
Four points on the graph of a polynomial P are shown in the table above. If P is a polynomial of degree 3, then P(x) could equal
View Solution