x−5−3−11y04−30
Four points on the graph of a polynomial P are shown in the table above. If P is a polynomial of degree 3, then P(x) could equal
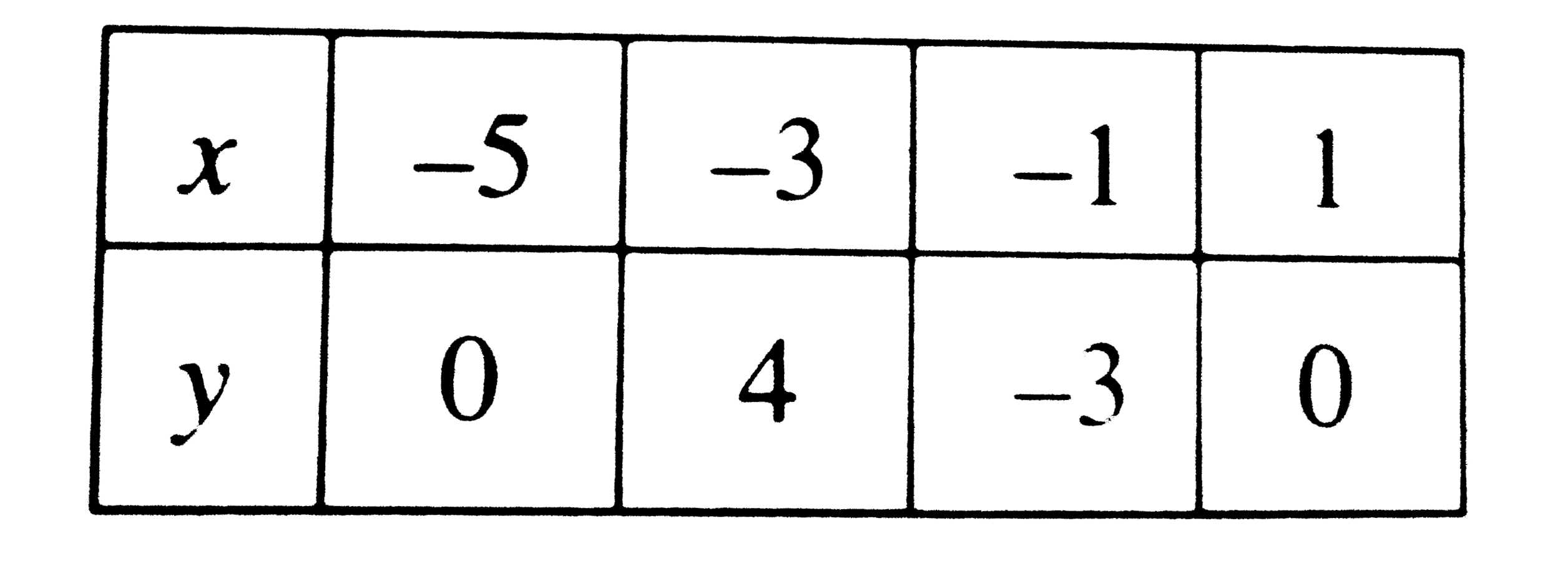
a(x-5)(x-2)(x+1)
a(x-5)(x+2)(x+1)
a(x+5)(x-2)(x-1)
a(x+5)(x+2)(x-1)
The correct Answer is:D
Since -5 and 1 are both zeros, (x+5) and (x-1) are factors of P(x). Since P(x) changes sign between x=-3 and x=-1, there is a zero between these two values. Choice D is the only one that meets all three criteria.
Topper's Solved these Questions
Similar Questions
Knowledge Check
For a polynomial p(x), the value of p(3) is −2.
Which of the following must be true about p(x) ?Ax−5 is a factor of p(x).Bx−2 is a factor of p(x).Cx+2 is a factor of p(x).DThe remainder when p(x) is divided by x−3 is−2.If p(x) is a polynomial function and p(-1)=3, which statement is true?
AThe remainder when p(x) is divided by x-3 is -1.BThe remainder when p(x) is divided by x+3 is -1.CThe remainder when p(x) is divided by x-1 is 3.DThe remainder when p(x) is divided by x+1 by 3.
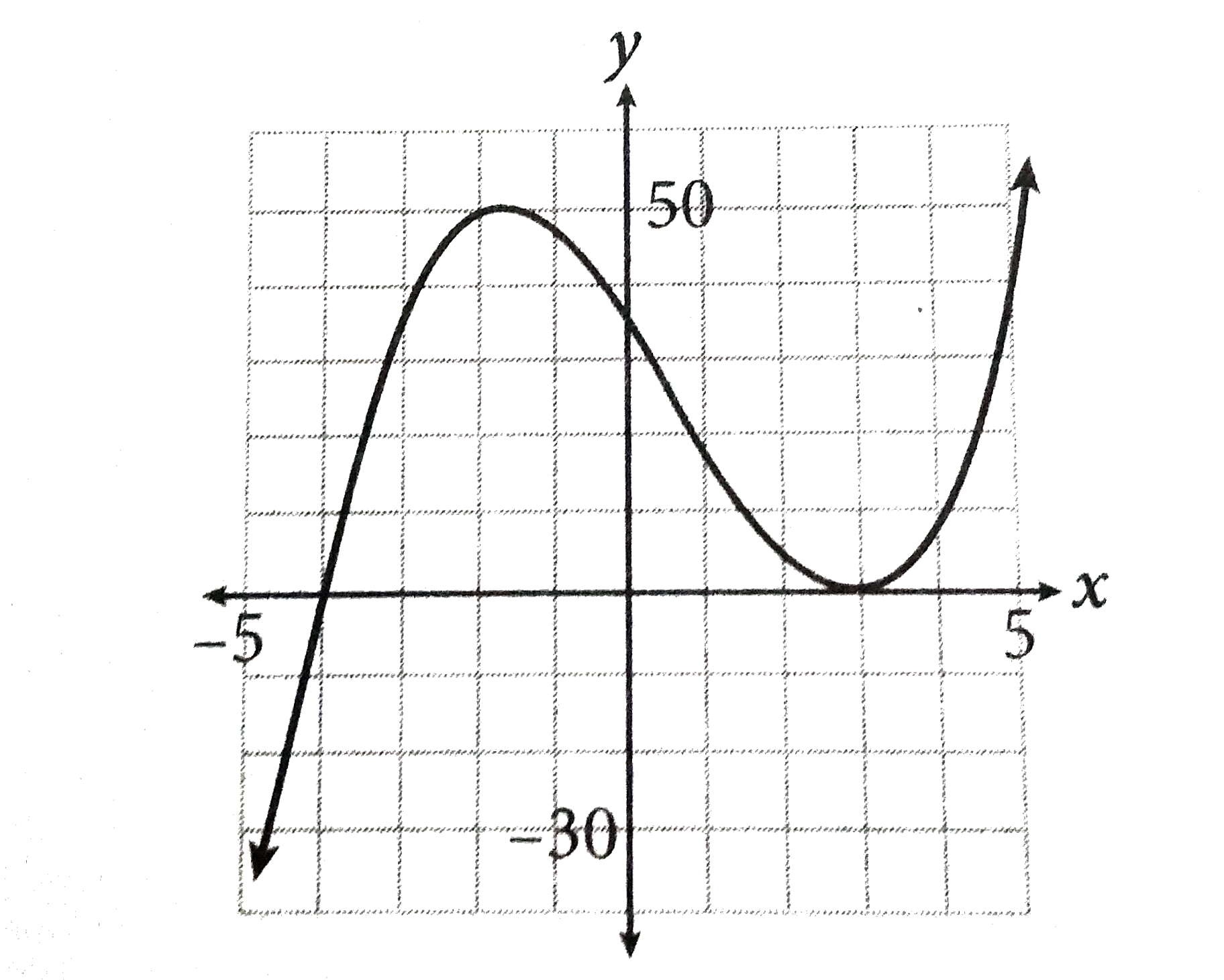
If p(x) is the polynomial functions shown in the graph above, which of the following could be fractored form of p(x)?
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The factor of the polynomial x3+3x2+4x+12 is
(1)x+3 (2)x−3 (3)x+2 (4)x−2
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
THe polynomials P(x)=kx3+3x2−3andQ(x)=2x3−5x+k, when divided by (x−4) leave the same remainder. Then the value of k is
View SolutionIf a is defined by f (x)=a0xn+a1xn−2+a2xn−2+...+an−1x+an where n is a non negative integer and a0,a1,a2,…….,an are real numbers and a0≠0, then f is called a polynomial function of degree n. For polynomials we can define the following theorem
(i) Remainder theorem: Let p(x) be any polynomial of degree greater than or equal to one and 'a' be a real number. if p(x) is divided by (x-a), then the remainder is equal to p(a).
(ii) Factor theorem : Let p(x) be a polynomial of degree greater than or equal to 1 and 'a' be a real number such that p(a) = 0, then (x-a) is a factor of p(x). Conversely, if (x-a) is a factor of p(x). then p(a)=0.
The remainder when the polynomial P(x)=x4−3x2+2x+1 is divided by x−1 is
View SolutionIf 1 is a zero of the polynomial p(x)=ax2—3(a—1)x−1, then find the value of a.
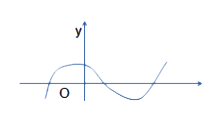
View SolutionThe following figure shows the graph of y=p(x), where p(x) is a polynomial in variable x. The number of zeroes of the polynomial p(x) is
View Solution
