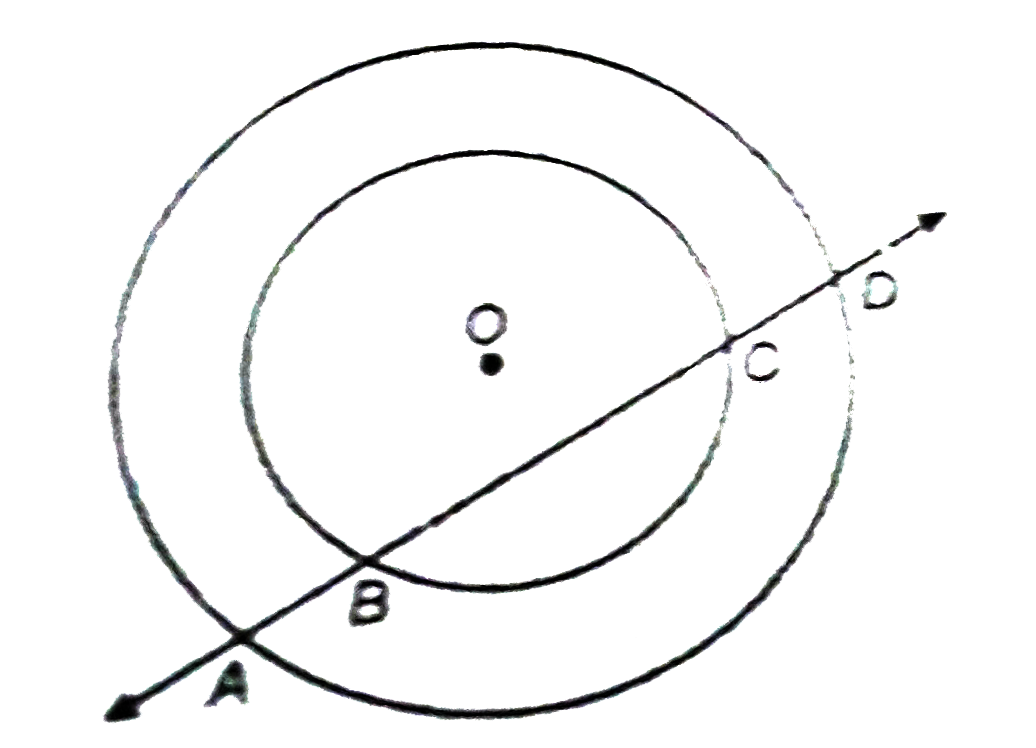
A straight line intersects thethree concentric circles at A, B, C. if the distance of line from the centre of the circles is 'P', prove that the area of the triangle formed by tangents to the circle at A, B, C is (12P.AB.BC.CA).
Step by step video & image solution for A straight line intersects thethree concentric circles at A, B, C. if the distance of line from the centre of the circles is 'P', prove that the area of the triangle formed by tangents to the circle at A, B, C is ((1)/(2P).AB.BC.CA). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
7 Videos
- DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS BOOK - ARIHANT MATHS ENGLISHCHAPTER - DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS EXERCISE - Exercise (Single Integer Answer Type Questions)
9 Videos
- DIFFERENTIATION BOOK - ARIHANT MATHS ENGLISHCHAPTER - DIFFERENTIATION EXERCISE - Exercise For Session 10
4 Videos
- ELLIPSEBOOK - ARIHANT MATHS ENGLISHCHAPTER - ELLIPSEEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
27 Videos
Similar Questions
Knowledge Check

The circle above with centre A has an area of 21. BC is tangent to the circle with centre A at point B. IF AC=2AB, then what is the area of the shaded region?A3.5B15.75C17.5D21
In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A,B,C and D . Show that AB=CD.
View SolutionThe extremities of a diagonal of a rectangle are (−4,4)and(6,−1). A circle circumscribes the rectangle and cuts an intercept AB on the y-axis. If Δ be the area of the triangle formed by AB and the tangents to the circle at AandB, then 8Δ=.
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionThe straight line x−2y+5=0 intersects the circle x2+y2=25 in points P and Q, the coordinates of the point of the intersection of tangents drawn at P and Q to the circle is
View SolutionA circle touches the line L and the circle C1 externally such that both the circles are on the same side of the line, then the locus of centre of the circle is :
View SolutionIn Figure, P, is any point on the chord BC of a circle such that AB=AP. Prove that CP=CQ.
View Solution