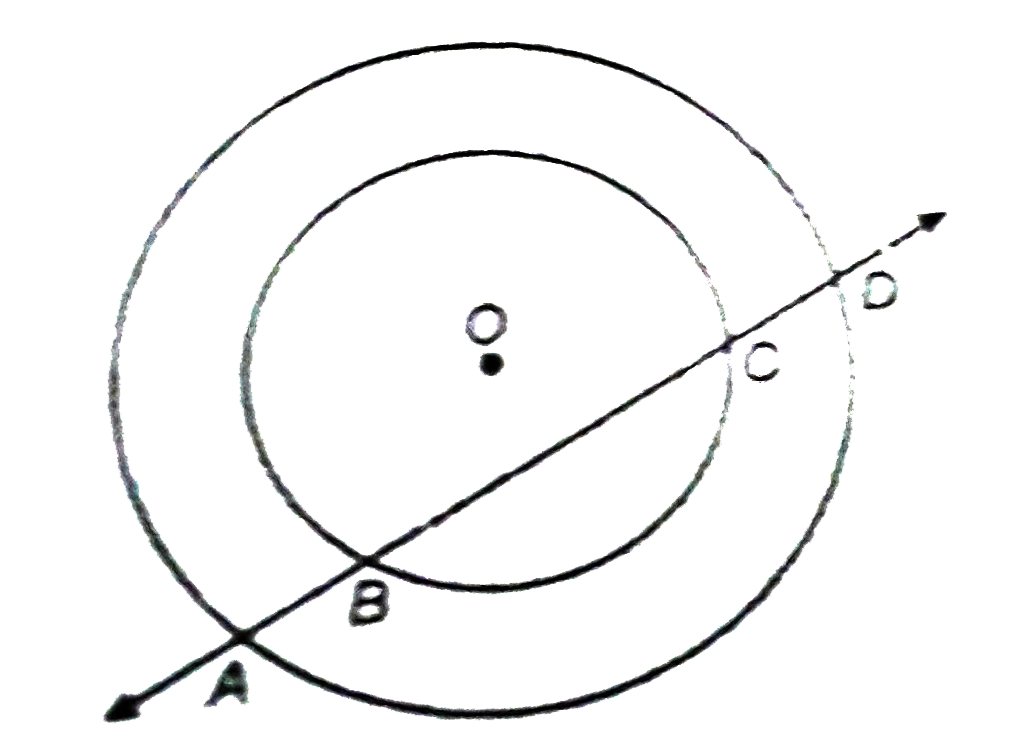
In Figure, is a line intersecting the two concentric circles, whose common centre is at the points and . Show that
To solve the problem, we need to show that the length of chord AB in the larger circle is equal to the length of chord CD in the smaller circle. Here’s a step-by-step solution:
Step 1: Identify the Setup
We have two concentric circles with a common center O. The line l intersects the larger circle at points A and B, and the smaller circle at points C and D.
Hint: Remember that concentric circles share the same center.
Step 2: Draw Perpendiculars
Draw a perpendicular line from the center O to the chords AB and CD. Let the perpendicular from O to chord AB meet AB at point M, and the perpendicular from O to chord CD meet CD at point N.
Hint: The property of circles states that a perpendicular from the center to a chord bisects the chord.
Step 3: Apply the Bisecting Property
Since OM is perpendicular to AB, we have:
- AM = MB (let’s call this length x)
Similarly, since ON is perpendicular to CD, we have:
- CN = ND (let’s call this length y)
Hint: Use the property of perpendiculars from the center to chords to establish equal segments.
Step 4: Relate the Chords
From the properties established:
- The length of chord AB can be expressed as:
AB=AM+MB=x+x=2x
- The length of chord CD can be expressed as:
CD=CN+ND=y+y=2y
Hint: Recognize that both chords can be expressed in terms of their respective segments.
Step 5: Show Equality
Since both chords are bisected by the perpendiculars from the center, we can conclude that:
- The distance from the center O to the chords is the same (since they are concentric), thus:
AM=CNandMB=ND
This implies that:
AB=CD
Hint: The equality of the segments derived from the center leads to the conclusion about the lengths of the chords.
Conclusion
Thus, we have shown that:
AB=CD
This completes the proof that the lengths of the chords AB and CD are equal.
---
We have two concentric circles with a common center O. The line l intersects the larger circle at points A and B, and the smaller circle at points C and D.
Draw a perpendicular line from the center O to the chords AB and CD. Let the perpendicular from O to chord AB meet AB at point M, and the perpendicular from O to chord CD meet CD at point N.
Since OM is perpendicular to AB, we have:
- AM = MB (let’s call this length x)
- CN = ND (let’s call this length y)
From the properties established:
- The length of chord AB can be expressed as:
AB=AM+MB=x+x=2x
- The length of chord CD can be expressed as:
CD=CN+ND=y+y=2y
Since both chords are bisected by the perpendiculars from the center, we can conclude that:
- The distance from the center O to the chords is the same (since they are concentric), thus:
AM=CNandMB=ND
This implies that:
AB=CD
Thus, we have shown that:
AB=CD
Topper's Solved these Questions
Similar Questions
In Figure, l is a line intersecting the two concentric circles, whose common centre is O, at the points A, B, C and D . Show that AB=CD.
View SolutionIf a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn the figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View SolutionIn Figure, line segments AB is parallel to another line segment CD.O is the mid-point of AD. Show that: AOB≅ DOC.
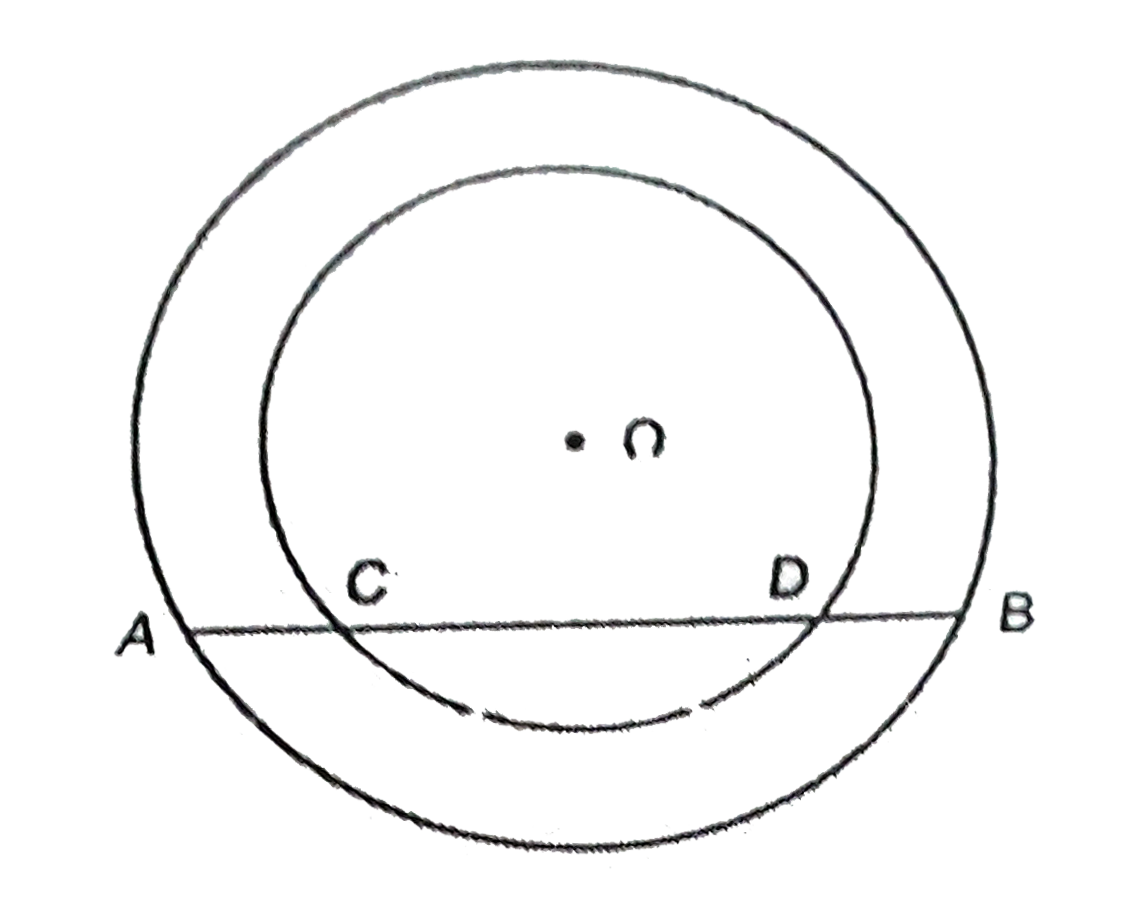
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View SolutionIn the Figure, OD is perpendicular to the chord AB of a circle whose centre is O. If BC is a diameter, show that CA=2OD.
View Solution