A regular pentagon and a regular decagon have the same perimeter, prove that their areas are as 2:√5.
The correct Answer is:=2(√5+1)5+√5=2√5
Step by step video & image solution for A regular pentagon and a regular decagon have the same perimeter, prove that their areas are as 2:sqrt5. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
A triangle and a regular hexagon have the same perimeter. If the area of the hexagon is 72√3, what is the area of the triangle ?
A62.354B83.138C101.823D103.923In the figure shown, ABCDEF is a regular hexagon and AOF is an equilateral triangle. The perimeter of ΔAOF is 2a feet. What is the perimeter of the hexagon in feet?
 A2aB3aC4aD6a
A2aB3aC4aD6a
If the sides of a regular pentagon are l, find the rule that gives the perimeter of the pentagon. Also, use rule to find the perimeter if the side of the pentagon is 7 cm.
View SolutionIf A1 and A2 be areas of two regular polygons having the same perimeter and number of sides be n and 2n respectively, then : A1A2 is
View SolutionIf the area of regular hexagon is 96√3, what is its perimeter?
View SolutionExpress the angular measurement of the angle of a regular decagon in the degrees and radians.
View SolutionIn the given figure , BD is a side of a regular hexagon. DC is a side of a regular pentagon and AD is a diameter , Calculate:
(i) ∠ADC,
(ii) ∠BDA
(iii) ∠ABC
(iv)∠AEC
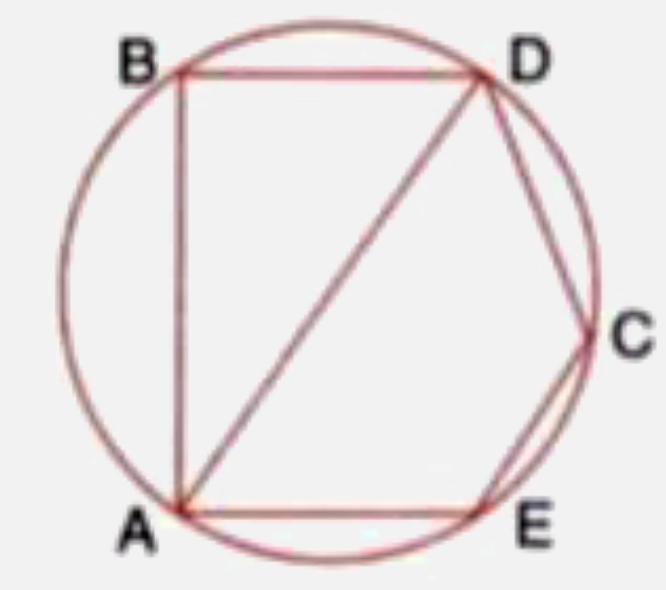
View SolutionProve that the interior angle of a regular pentagon is three times the exterior angle of a regular decagon.
View Solution
