In any ΔABC, if D be any points of the base BC such that BDDC=mnand∠ABD=α,∠DAC=β,∠CDA=θandAD=x then prove that
(m+n)2.x=(m+n)(mb2+nc2)−mna2
The correct Answer is:(m+n)2.+mna2m+n=mb2+nc2(nb2+nc2)−mna2
To prove the equation (m+n)2⋅x=(m+n)(mb2+nc2)−mna2, we will follow a systematic approach using the properties of triangles and the given conditions.
1. Set Up the Ratios:
Given that BDDC=mn, we can express BD and DC in terms of a (the length of BC):
BD=amm+n,DC=anm+n
This gives us the lengths of segments BD and DC in terms of a.
Hint: Use the given ratio to express segments in terms of a common base length.
2. Apply the Law of Cosines:
For triangle ABD:
AB2=AD2+BD2−2⋅AD⋅BD⋅cos(α)
Substituting AB=c, AD=x, and BD=amm+n:
c2=x2+(amm+n)2−2x⋅amm+n⋅cos(α)
Hint: Remember to apply the Law of Cosines correctly for the triangle.
3. For Triangle ACD:
Similarly, for triangle ACD:
AC2=AD2+DC2−2⋅AD⋅DC⋅cos(β)
Substituting AC=b, AD=x, and DC=anm+n:
b2=x2+(anm+n)2−2x⋅anm+n⋅cos(β)
Hint: Use the Law of Cosines again for the second triangle.
4. Combine the Equations:
Now, we have two equations:
c2=x2+(amm+n)2−2x⋅amm+n⋅cos(α)
b2=x2+(anm+n)2−2x⋅anm+n⋅cos(β)
Multiply the first equation by m and the second by n:
mc2=mx2+m(amm+n)2−2mx⋅amm+n⋅cos(α)
nb2=nx2+n(anm+n)2−2nx⋅anm+n⋅cos(β)
Hint: Make sure to multiply correctly and keep track of the terms.
5. Sum the Equations:
Adding both equations:
mb2+nc2=(m+n)x2+m(amm+n)2+n(anm+n)2−2x(m⋅a⋅cos(α)+n⋅a⋅cos(β)m+n)
Hint: This step combines the results from both triangles.
6. Substitute and Rearrange:
Rearranging gives:
(m+n)x2=mb2+nc2−(mn⋅a2(m+n)2)
This leads us to:
(m+n)2x=(m+n)(mb2+nc2)−mna2
Hint: Ensure that all terms are correctly placed on either side of the equation.
Conclusion:
Thus, we have proven that:
(m+n)2⋅x=(m+n)(mb2+nc2)−mna2
Given that BDDC=mn, we can express BD and DC in terms of a (the length of BC):
BD=amm+n,DC=anm+n
This gives us the lengths of segments BD and DC in terms of a.
For triangle ABD:
AB2=AD2+BD2−2⋅AD⋅BD⋅cos(α)
Substituting AB=c, AD=x, and BD=amm+n:
c2=x2+(amm+n)2−2x⋅amm+n⋅cos(α)
Similarly, for triangle ACD:
AC2=AD2+DC2−2⋅AD⋅DC⋅cos(β)
Substituting AC=b, AD=x, and DC=anm+n:
b2=x2+(anm+n)2−2x⋅anm+n⋅cos(β)
Now, we have two equations:
c2=x2+(amm+n)2−2x⋅amm+n⋅cos(α)
b2=x2+(anm+n)2−2x⋅anm+n⋅cos(β)
Multiply the first equation by m and the second by n:
mc2=mx2+m(amm+n)2−2mx⋅amm+n⋅cos(α)
nb2=nx2+n(anm+n)2−2nx⋅anm+n⋅cos(β)
Adding both equations:
mb2+nc2=(m+n)x2+m(amm+n)2+n(anm+n)2−2x(m⋅a⋅cos(α)+n⋅a⋅cos(β)m+n)
Rearranging gives:
(m+n)x2=mb2+nc2−(mn⋅a2(m+n)2)
This leads us to:
(m+n)2x=(m+n)(mb2+nc2)−mna2
Thus, we have proven that:
(m+n)2⋅x=(m+n)(mb2+nc2)−mna2
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES1videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 120videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)51videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
SEQUENCES AND SERIES
Similar Questions
In ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2ADView SolutionIn a quadrilateral ABCD ∠B=∠D=90∘ Prove that : 2AC2−BC2=AB2+AD2+DC2
View SolutionIf
xcosA+ysinA=mandxsinA−ycosA=n,
then prove that :
x2+y2=m2+n2View SolutionIf cosecθ−sinθ=m and secθ−cosθ=n, prove that (m2n)23+(mn2)23=1
View SolutionWhat should be added to m2−2mn+5n2 to get n2+mn−m2?
View SolutionIn triangle ABC, D is a point in side BC such that 2BD=3DC. Prove that the area of triangle ABD = 35×Area ofΔABC
View SolutionIn triangle ABC, angle A=90∘,CA=AB and D is a point on AB produced. Prove that:
DC2−BD2=2AB.AD.
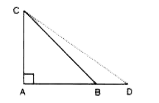 View Solution
View SolutionABC is a triangle, right angled at B, M is a point on BC. Prove that :
AM2+BC2=AC2+BM2
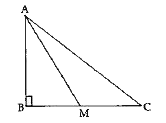 View Solution
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CDView SolutionProve that:tan−1(mn)+tan−1(n−mn+m)=[π4;m2n2>−1
View Solution

