Given an isoceles triangle with equal side of length b and angle $α < π / 4$ , then
the inradius r is given by

A

$R = \frac{1}{2} b cos e c α$

B

$Δ = 2 b^{2} sin 2 α$

C

$r = \frac{b sin 2 α}{2 (1 + cos α)}$

D

$O I ∣ ∣ ∣ ∣ ∣ \frac{b cos (\frac{3 α}{2})}{2 sin α (\frac{α}{2})} ∣ ∣ ∣ ∣ ∣$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C, D

|

Answer

Step by step video & image solution for Given an isoceles triangle with equal side of length b and angle alpha lt pi//4, then the inradius r is given by by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROPERTIES AND SOLUTION OF TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The lengths of the triangle shown below are rounded to the nearest 0.1 cm. What is the area, to the nearest $1 c m^{2}$ of the triangle?

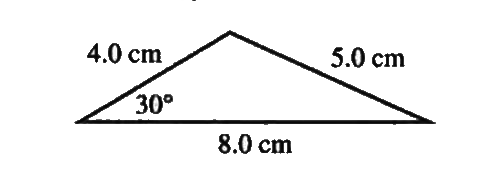
Note: The area of any triangle with sides of length a, b and c opposite angle of measure A, B, and C, respectively, is given by $\frac{1}{2} a b sin C$ .
A4
B5
C8
D10

ARIHANT MATHS ENGLISH-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (More Than One Correct Option Type Questions)

Home
Ask Doubt
Profile