In an acute angled triangle ABC, let AD,BE and CF be the perpendicular opposite sides of the triangle. The ratio of the product of the side lengths of the triangles DEF and ABC, is equal to
A. 3(abc)134(a+b+c)
B. 14
C. cosAcosBcosC
D. sin(A2)sin(B2)sin(C2)
The correct Answer is:C
To solve the problem, we need to find the ratio of the product of the side lengths of triangle DEF to the product of the side lengths of triangle ABC. Let's go through the steps systematically:
Step 1: Understand the Triangles
We have an acute-angled triangle ABC with perpendiculars AD, BE, and CF dropped from vertices A, B, and C to the opposite sides BC, CA, and AB respectively. The points D, E, and F are the feet of these perpendiculars, forming triangle DEF.
Step 2: Identify the Sides of Triangle DEF
Using properties of the pedal triangle, we know the lengths of the sides of triangle DEF can be expressed in terms of the circumradius R and the angles of triangle ABC:
- DE=R⋅sin(2C)
- EF=R⋅sin(2A)
- DF=R⋅sin(2B)
Step 3: Calculate the Product of the Sides of Triangle DEF
Now, we can calculate the product of the sides of triangle DEF:
DE⋅EF⋅DF=(R⋅sin(2C))⋅(R⋅sin(2A))⋅(R⋅sin(2B))=R3⋅sin(2A)⋅sin(2B)⋅sin(2C)
Step 4: Identify the Sides of Triangle ABC
For triangle ABC, we denote the sides as:
- a=BC
- b=CA
- c=AB
Using the sine rule, we can express the sides in terms of the circumradius R:
- a=2R⋅sinA
- b=2R⋅sinB
- c=2R⋅sinC
Step 5: Calculate the Product of the Sides of Triangle ABC
Now we calculate the product of the sides of triangle ABC:
a⋅b⋅c=(2R⋅sinA)⋅(2R⋅sinB)⋅(2R⋅sinC)=8R3⋅sinA⋅sinB⋅sinC
Step 6: Find the Ratio
Now we can find the ratio of the product of the sides of triangle DEF to the product of the sides of triangle ABC:
Ratio=DE⋅EF⋅DFa⋅b⋅c=R3⋅sin(2A)⋅sin(2B)⋅sin(2C)8R3⋅sinA⋅sinB⋅sinC
Step 7: Simplify the Ratio
We can simplify this expression:
Ratio=sin(2A)⋅sin(2B)⋅sin(2C)8⋅sinA⋅sinB⋅sinC
Using the identity sin(2A)=2sinAcosA, we can further simplify:
Ratio=2sinAcosA⋅2sinBcosB⋅2sinCcosC8sinAsinBsinC
This simplifies to:
Ratio=cosA⋅cosB⋅cosC
Final Answer
Thus, the ratio of the product of the side lengths of triangle DEF to the product of the side lengths of triangle ABC is:
cosA⋅cosB⋅cosC
We have an acute-angled triangle ABC with perpendiculars AD, BE, and CF dropped from vertices A, B, and C to the opposite sides BC, CA, and AB respectively. The points D, E, and F are the feet of these perpendiculars, forming triangle DEF.
Using properties of the pedal triangle, we know the lengths of the sides of triangle DEF can be expressed in terms of the circumradius R and the angles of triangle ABC:
- DE=R⋅sin(2C)
- EF=R⋅sin(2A)
- DF=R⋅sin(2B)
Now, we can calculate the product of the sides of triangle DEF:
DE⋅EF⋅DF=(R⋅sin(2C))⋅(R⋅sin(2A))⋅(R⋅sin(2B))=R3⋅sin(2A)⋅sin(2B)⋅sin(2C)
For triangle ABC, we denote the sides as:
- a=BC
- b=CA
- c=AB
- a=2R⋅sinA
- b=2R⋅sinB
- c=2R⋅sinC
Now we calculate the product of the sides of triangle ABC:
a⋅b⋅c=(2R⋅sinA)⋅(2R⋅sinB)⋅(2R⋅sinC)=8R3⋅sinA⋅sinB⋅sinC
Now we can find the ratio of the product of the sides of triangle DEF to the product of the sides of triangle ABC:
Ratio=DE⋅EF⋅DFa⋅b⋅c=R3⋅sin(2A)⋅sin(2B)⋅sin(2C)8R3⋅sinA⋅sinB⋅sinC
We can simplify this expression:
Ratio=sin(2A)⋅sin(2B)⋅sin(2C)8⋅sinA⋅sinB⋅sinC
Using the identity sin(2A)=2sinAcosA, we can further simplify:
Ratio=2sinAcosA⋅2sinBcosB⋅2sinCcosC8sinAsinBsinC
This simplifies to:
Ratio=cosA⋅cosB⋅cosC
Thus, the ratio of the product of the side lengths of triangle DEF to the product of the side lengths of triangle ABC is:
cosA⋅cosB⋅cosC
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS3videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Single Integer Answer Type Questions)15videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)11videos
PROPERTIES AND SOLUTION OF TRIANGLES
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)51videos
PRODUCT OF VECTORS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)38videos
SEQUENCES AND SERIES
Similar Questions
Knowledge Check
- Question 1 - Select One
AD is the longest side of the triangle ABD shown in the figure. What is the length side of ΔABC ?
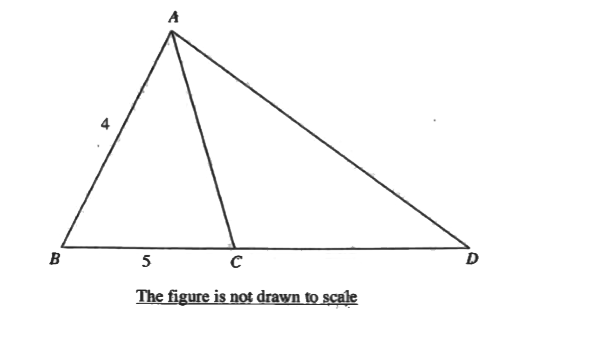 A2B3C√41D9
A2B3C√41D9
In an acute angle ΔABC, let AD, BE and CF be the perpendicular from A, B and C upon the opposite sides of the triangle. (All symbols used have usual meaning in a tiangle.)
The orthocentre of the ΔABC, is theView SolutionIn an acute angle triangle ABC, AD, BE and CF are the altitudes, then EFa+FDb+DEc is equal to -
View SolutionIf D id the mid-point of the side BC of a triangle ABC and AD is perpendicular to AC , then
View SolutionProve that the perpendicular let fall from the vertices of a triangle to the opposite sides are concurrent.
View SolutionConsider a triangle ABC, and that AA', BB', CC' be the perpendicular form A, B and C upon the sides opposite to them. These three perpendicualrs meets in H, called the orthocenter of the triangle.The triangle A'B'C' formed by the feet of the perpendicular is called the pedal triangle of ABC. (Assume ∠A,B,C≠90∘)

Suppose the triangle ABC have angles 60∘,70∘ and 50∘. Then the pedal triangle A'B'C' have angles given byView SolutionThe sides of triangle are in A.P. and the greatest angle exceeds the least by 90∘. The sides are in the ratio:
View SolutionIf the lengths of the sides of a triangle are in AP and the greatest angle is double the smallest, then a ratio of lengths of the sides of this triangle is
View Solution

