If (1+x)n=n∑r=0Cr,xr, then prove that
(∑∑)0≤i<j≤n(iCi+jCj)=n22n∑r=01Cr .
To prove the given statement, we will follow a systematic approach. Let's denote the expression we want to prove as S:
S=∑0≤i<j≤n(1Ci+1Cj)
where Cr=(nr).
Step 1: Rewrite the expression for S
We can express S as:
S=∑0≤i<j≤n1Ci+∑0≤i<j≤n1Cj
Since the two sums are symmetric, we can combine them:
S=∑0≤i<j≤n1Ci+∑0≤j<i≤n1Cj=2∑0≤i<j≤n1Ci
Step 2: Change the limits of the summation
Now we can change the limits of summation. The total number of ways to choose i and j such that i<j is half of the total combinations of n elements taken 2 at a time. Therefore, we can express S as:
S=n∑i=0n∑j=01Ci⋅1Cj−n∑i=01Ci
Step 3: Calculate the double sum
We know that:
n∑i=01Ci=n∑r=01(nr)=n∑r=0rn⋅Cr
Now, we can express the double sum as:
n∑i=0n∑j=01Ci⋅1Cj=(n∑r=01Cr)2
Step 4: Substitute back into S
Substituting back into our expression for S:
S=12(n∑r=01Cr)2−n∑r=01Cr
Step 5: Use the identity for Cr
Using the identity Cr=(nr), we can relate it to n2:
S=n22n∑r=01Cr
Conclusion
Thus, we have shown that:
∑0≤i<j≤n(1Ci+1Cj)=n22n∑r=01Cr
This completes the proof.
Topper's Solved these Questions
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - JEE Type Solved Example : (Matching Type Questions )
2 Videos
- BIONOMIAL THEOREMBOOK - ARIHANT MATHS ENGLISHCHAPTER - BIONOMIAL THEOREMEXERCISE - Exercise For Session 1
7 Videos
- AREA OF BOUNDED REGIONSBOOK - ARIHANT MATHS ENGLISHCHAPTER - AREA OF BOUNDED REGIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
23 Videos
- CIRCLE BOOK - ARIHANT MATHS ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
16 Videos
Similar Questions
Find the sum (∑∑)0≤i<j≤nnCi.
View SolutionFind the value of (∑∑)0≤i<j≤n(1+j)(nCi+nCj).
View Solution(1+x)n=n∑r=0Crxr then match the following
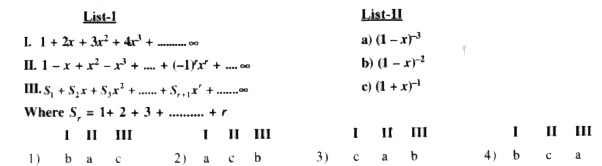
View SolutionFind the value of ∑∑0≤i<j≤n(nCi+nCj).
View SolutionIf (1+x)n=n∑r=0Crxr,(1+C0C1)(1+C2C1)...(1+CnCn−1) is equal to
View Solutionn−1∑r=0CrCr+Cr+1=
View SolutionIf (1+x)n=n∑r=0Crxr, then prove that C1+2C2+3C3+....+nCn=n2n−1. .
View SolutionIf (1+x)n=C0+C1x+C2x2+….+Cnxn, then the value of ∑∑0≤r<s≤n(r+s)(Cr+Cs) is :
View SolutionIf an=n∑r=01nCr , find the
value of n∑r=0rnCr
View SolutionLet (1+x)n=n∑r=0Crxr and ,
C1C0+2C2C1+C3C2+…+nCnCn−1=1kn(n+1),
then the value of k, is
View Solution
